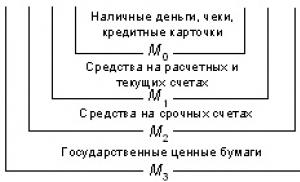
Сначала идет деление или сложение. Порядок выполнения действий

Составление выражения со скобками

1. Составь из следующих предложений выражения со скобками и реши их.

Из числа 16 вычти сумму чисел 8 и 6.
Из числа 34 вычти сумму чисел 5 и 8.
Сумму чисел 13 и 5 вычесть из числа 39.
Разность чисел 16 и 3 прибавь к числу 36
Разность чисел 48 и 28 прибавь к числу 16.

2. Реши задачи, сперва составив правильно выражения, а за тем последовательно их решив:

2.1. Папа принёс из леса мешок с орехами. Коля взял из мешка 25 орешков и съел. За тем Маша взяла из мешка 18 орешков. Мама то же взяла из мешка 15 орешков, но положила обратно 7 из них. Сколько осталось в итоге орешков в мешке, если в начале их было 78?

2.2. Мастер ремонтировал детали. В начале рабочего дня их было 38. В первой половине дня он смог отремонтировать 23 из них. После полудня ему принесли еще столько же, сколько было в самом начале дня. Во второй половине он отремонтировал еще 35 деталей. Сколько деталей ему осталось отремонтировать?

3. Реши примеры правильно выполняя последовательность действий:

45: 5 + 12 * 2 -21:3
56 - 72: 9 + 48: 6 * 3
7 + 5 * 4 - 12: 4
18: 3 - 5 + 6 * 8

Решение выражений со скобками

1. Реши примеры правильно раскрывая скобки:

1 + (4 + 8) =	8 - (2 + 4) =	3 + (6 - 5) =	59 + 25 =
82 + 14 =	29 + 52 =	18 + 47 =	39 + 53 =
37 + 53 =	25 + 63 =	87 + 17 =	19 + 52 =

2. Реши примеры правильно выполняя последовательность действий:

2.1. 36: 3 + 12 * (2 - 1) : 3
2.2. 39 - (81: 9 + 48: 6) * 2
2.3. (7 + 5) * 2 - 48: 4
2.4. 18: 3 + (5 * 6) : 2 - 4

3. Реши задачи, сперва составив правильно выражения, а за тем последовательно их решив:

3.1. На складе было 25 упаковок стирального порошка. В один магазин увезли 12 упаковок. За тем во второй магазин увезли столько же. После этого на склад привезли в 3 раза больше упаковок, чем было раньше. Сколько упаковок порошка стало на складе?

3.2. В гостинице проживало 75 туристов. За первый день из гостиницы уехали 3 группы по 12 человек, а заехали 2 группы по 15 человек. На второй день уехали еще 34 человека. Сколько туристов осталось в гостинице к концу 2 дня?

3.3. В химчистку привезли 2 мешка одежды по 5 вещей в каждом мешке. За тем забрали 8 вещей. После полудня привезли ещё 18 вещей на стирку. А забрали только 5 выстиранных вещей. Сколько вещей в химчистке к концу дня, если в начале дня там было 14 вещей?

ФИ _________________________________

21: 3 * 6 - (18 + 14) : 8 =	63: (81: 9) + (8 * 7 - 2) : 6 =	64:2: 4+ 9*7-9*1=
37 *2 + 180: 9 – 36: 12 =	52 * 10 – 60: 15 * 1 =	72: 4 +58:2=
5 *0: 25 + (72: 1 – 0) : 9 =	21: (3 * 7) – (7* 0 + 1)*1 =	6:6+0:8-8:8=
91: 7 + 80: 5 – 5: 5 =	64:4 - 3*5 +80:2=	(19*5 – 5) : 30 =
19 + 17 * 3 – 46 =	(39+29) : 4 + 8*0=	(60-5) : 5 +80: 5=
54 – 26 + 38: 2 =	63: (7*3) *3=	(160-70) : 18 *1=
200 – 80: 5 + 3 * 4 =	(29+25): (72:8)=	72:25 + 3* 17=
80: 16 + 660: 6 =	3 * 290 – 800=	950:50*1-0=
(48: 3) : 16 * 0 =	90-6*6+29=	5* (48-43) +15:5*7=
54: 9 *8 - 14: 7 * 4 =	63: 7*4+70:7 * 5=	24: 6*7 - 7*0=
21: 7 * 8 + 32: 8 * 4 =	27: 3* 5 + 26-18 *4=	54: 6*7 - 0:1=
45: 9 * 6 + 7 * 5 – 26 =	28: 7 *9 + 6 * (54 – 47)=	6*(9: 3) - 40:5 =
21 * 1 - 56: 7 – 8 =	9 * (64: 8) - 18:18	3 *(14: 2) - 63:9=
4 * 8 + 42: 6 *5 =	0*4+0:5 +8* (48: 8)=	56:7 +7*6 - 5*1=
31 * 3 - 17 – 80: 16 * 1 =	57:19 *32 - 11 *7=	72-96:8 +60:15 *13=
36 + 42: 3 + 23 + 27 *0 =	56:14 *19 - 72:18=	(86-78:13)* 4=
650 – 50 * 4 + 900: 100 =	630: 9 + 120 * 5 + 40=	980 – (160 + 20) : 30=
940 - (1680 – 1600) * 9 =	29* 2+26 – 37:2=	72:3 +280: (14*5)=
300: (5 *60) * (78: 13) =	63+ 100: 4 – 8*0=	84:7+70:14 – 6:6=
45: 15 – 180: 90 + 84: 7 =	32+51 + 48:6 * 5=	54:6 ?2 – 70:14=
38: 2 – 48: 3 + 0 * 9 =	30:6 * 8 – 6+3*2=	(95:19) *(68:2)=
(300 - 8 * 7) * 10 =	1:1 - 0*0 + 1*0 - 1*1=	(80: 4 – 60:30) *5 =
2 * (120: 6 – 80: 20) =	56:4+96:3- 0*7=	20+ 20: 4 - 1*5=
(18 + 14) : 8 – (7 *0 + 1) *1 =	(8*7-2):6 +63: (7*3)=	(50-5) : 5+21: (3*7)=
19 + 17 * 3 – 60: 15 * 1 =	80: 5 +3*5 +80:2=	54: 9 *8-64:4 +16*0=
72 * 10 - 64: 2: 4 =	84 – 36 + 38:2	91:13+80:5 – 5:5
300 – 80: 5 + 6 * 4 =	950:190 *1+14: 7*4=	(39+29) : 17 + 8*0=
(120 - 30) : 18 * 1- 72: 25 =	210:30*60-0:1=	90-6*7+3* 17=
240: 60 *7 – 7 * 0 =	60:60+0:80-80:80=	720: 40 +580:20=
9 *7 – 9 *1 + 5 * 0: 25 =	21: 7 * 6 +32: 4 *5=	80:16 +66:6 -63:(81:9)=
(19 * 5 – 5) : 30 + 70: 7 =	15:5*7 + 63: 7 * 5=	54: 6 * 7 - (72:1-0):9=
3 *290 – 600 – 5 * (48 – 43) =	(300-89*7)*10 - 3?2=	(80: 4) +30*2+ 180: 9=
30: 6 * 8 – 6 + 48: 3 + 0 *9 =	(95:19) *(68:34) - 60:30*5=	27: 3*5 - 48:3=
3* 290 – 800 + 950: 50 =	80:16 +660:6*1-0=	90-6*6+ 15:5*7=
5*(48 - 43) + (48: 3) :16*0=	280: (14*5) +630: 9*0=	300: (50*6)* (78: 6)=

Если в примерах встретится вопросительный знак (?), следует его заменить на знак * - умножение.

1. РЕШИ ВЫРАЖЕНИЯ:

35: 5 + 36: 4 - 3
26 + 6 х 8 – 45: 5 24: 6 + 18 – 2 х 6
9 х 6 – 3 х 6 + 19 – 27:3

2. РЕШИ ВЫРАЖЕНИЯ:

48: 8 + 32 – 54: 6 + 7 х 4
17 + 24: 3 х 4 – 27: 3 х 2 6 х 4: 3 + 54: 6: 3 х 6 + 2 х 9
100 – 6 х 2: 3 х 9 – 39 + 7 х 4

3. РЕШИ ВЫРАЖЕНИЯ:

100 – 27: 3 х 6 + 7 х 4
2 х 4 + 24: 3 + 18: 6 х 9 9 х 3 – 19 + 6 х 7 – 3 х 5
7 х 4 + 35: 7 х 5 – 16: 2: 4 х 3

4. РЕШИ ВЫРАЖЕНИЯ:

32: 8 х 6: 3 + 6 х 8 – 17
5 х 8 – 4 х 7 + 13 - 11 24: 6 + 18: 2 + 20 – 12 + 6 х 7
21: 3 – 35: 7 + 9 х 3 + 9 х 5

5. РЕШИ ВЫРАЖЕНИЯ:

42: 7 х 3 + 2 + 24: 3 – 7 + 9 х 3
6 х 6 + 30: 5: 2 х 7 - 19 90 - 7 х 5 – 24: 3 х 5
6 х 5 – 12: 2 х 3 + 49

6. РЕШИ ВЫРАЖЕНИЯ:

32: 8 х 7 + 54: 6: 3 х 5
50 – 45: 5 х 3 + 16: 2 х 5 8 х 6 + 23 – 24: 4 х 3 + 17
48: 6 х 4 + 6 х 9 – 26 + 13

7. РЕШИ ВЫРАЖЕНИЯ:

42: 6 + (19 + 6) : 5 – 6 х 2
60 – (13 + 22) : 5 – 6 х 4 + 25 (27 – 19) х 4 + 18: 3 + (8 + 27) :5 -17
(82 – 74) : 2 х 7 + 7 х 4 - (63 – 27): 4
8. РЕШИ ВЫРАЖЕНИЯ:

90 – (40 – 24: 3) : 4 х 6 + 3 х 5
3 х 4 + 9 х 6 – (27 + 9) : 4 х 5
(50 – 23) : 3 + 8 х 5 – 6 х 5 + (26 + 16) : 6
(5 х 6 – 3 х 4 + 48: 6) +(82 – 78) х 7 – 13
54: 9 + (8 + 19) : 3 – 32: 4 – 21: 7 + (42 – 14) : 4 – (44 14) : 5

9. РЕШИ ВЫРАЖЕНИЯ:

9 х 6 – 6 х 4: (33 – 25) х 7
3 х (12 – 8) : 2 + 6 х 9 - 33 (5 х 9 - 25) : 4 х 8 – 4 х 7 + 13
9 х (2 х 3) – 48: 8 х 3 + 7 х 6 - 34

10. РЕШИ ВЫРАЖЕНИЯ:

(8 х 6 – 36: 6) : 6 х 3 + 5 х 9
7 х 6 + 9 х 4 – (2 х 7 + 54: 6 х 5) (76 – (27 + 9) + 8) : 6 х 4
(7 х 4 + 33) – 3 х 6:2

11. РЕШИ ВЫРАЖЕНИЯ:

(37 + 7 х 4 – 17) : 6 + 7 х 5 + 33 + 9 х 3 – (85 – 67) : 2 х 5
5 х 7 + (18 + 14) : 4 – (26 – 8) : 3 х 2 – 28: 4 + 27: 3 – (17 + 31) : 6

12. РЕШИ ВЫРАЖЕНИЯ:

(58 – 31) : 3 – 2 + (58 – 16) : 6 + 8 х 5 – (60 – 42) : 3 + 9 х 2
(9 х 7 + 56: 7) – (2 х 6 – 4) х 3 + 54: 9

13. РЕШИ ВЫРАЖЕНИЯ:

(8 х 5 + 28: 7) + 12: 2 – 6 х 5 + (13 – 5) х 4 + 5 х 4
(7 х 8 – 14: 7) + (7 х 4 + 12: 6) – 10: 5 + 63: 9

Тест «Порядок арифметических действий» (1 вариант)
1(1б)
2(1б)
3(1б)
4(3б)
5(2б)
6(2б)
7(1б)
8(1б)
9(3б)
10(3б)
11(3б)
12(3б)

110 – (60 +40) :10 х 8




а) 800 б) 8 в) 30

а) 3 4 6 5 2 1 4 5 6 3 2 1

3 4 6 5 1 2

5. В каком из выражений последнее действие умножение?
а) 1001:13 х (318 +466) :22

в) 10000 – (5 х 9+56 х 7) х2
6. В каком из выражений первое действие вычитание?
а) 2025:5 – (524 – 24:6) х45
б) 5870 + (90-50 +30) х8 -90
в) 5400:60 х (3600:90 -90)х5




Выбери верный ответ:
9. 90 – (50- 40:5) х 2+ 30
а) 56 б) 92 в) 36
10. 100- (2х5+6 - 4х4) х2
а) 100 б) 200 в) 60
11. (10000+10000:100 +400) : 100 +100
а) 106 б) 205 в) 0
12. 150: (80 – 60:2) х 3
а) 9 б) 45 в) 1

Тест «Порядок арифметических действий»
1(1б)
2(1б)
3(1б)
4(3б)
5(2б)
6(2б)
7(1б)
8(1б)
9(3б)
10(3б)
11(3б)
12(3б)
1. Какое действие в выражении сделаешь первым?
560 – (80+20) :10 х7
а) сложение б) деление в) вычитание
2. Какое действие в этом же выражении сделаешь вторым?
а) вычитание б) деление в) умножение
3. Выбери правильный вариант ответа данного выражения:
а) 800 б) 490 в) 30
4. Выбери верный вариант расстановки действий:
а) 3 4 6 5 2 1 4 5 6 3 2 1
320: 8 х 7 + 9 х (240 – 60:15) в) 320:8 х 7+9х(240 – 60:15)

3 4 6 5 2 1
б) 320: 8 х 7 + 9 х (240 – 60:15)
5. В каком из выражений последнее действие деление?
а) 1001:13 х (318 +466) :22
б) 391 х37:17 х (2248:8 – 162)
в) 10000 – (5 х 9+56 х 7) х2
6. В каком из выражений первое действие сложение?
а) 2025:5 – (524 + 24 х6) х45
б) 5870 + (90-50 +30) х8 -90
в) 5400:60 х (3600:90 -90)х5
7. Выбери верное высказывание: «В выражении без скобок действия выполняются:»
а) по порядку б) х и: , затем + и - в) + и -, затем х и:
8. Выбери верное высказывание: «В выражении со скобками действия выполняются:»
а) сначала в скобках б)х и:, затем + и - в) по порядку записи
Выбери верный ответ:
9. 120 – (50- 10:2) х 2+ 30
а) 56 б) 0 в) 60
10. 600- (2х5+8 - 4х4) х2
а) 596 б) 1192 в) 60
11. (20+20000:2000 +30) : 20 +200
а) 106 б) 203 в) 0
12. 160: (80 – 80:2) х 3
а) 120 б) 0 в) 1

Особенно сложны и трудны были в старину действия умножения и деления – особенно последнее.

«Умножение – мое мучение, а с делением – беда», - говорили в старину.

В глубокой древности и почти до восемнадцатого века русские люди в своих вычислениях обходились без умножения и деления: они применяли лишь два арифметических действия - сложение и вычитание, да ещё так называемые «удвоения» и «раздвоение». Сущность русского старинного способа умножения состоит в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам (последовательное раздвоение) при одновременном удвоении другого числа. Если в произведении, например 24∙5, множимое уменьшить в 2 раза («раздвоить»), а множитель увеличить в 2 раза («удвоить»), то произведение не изменится: 24∙5=12∙10=120

Деление множимого продолжают до тех пор, пока в частном не получится 1, одновременно удваивая множитель. Последнее удвоенное число и дает искомый результат. Значит 32∙17=1∙544=544. В предлагаемом примере, все числа делятся на 2 без остатка.

А как быть, если деление на 2 происходит с остатком?

Если множимое не делится на 2, то от него сначала отнимается единица, а затем уже производится деление на 2. Строчки с четными множимыми вычеркиваются, а правые части строчек с нечетными множимыми складываются.

То есть 21∙17=(20+1)∙17=20∙17+1∙17.

Число 17 запомним (первая строка не вычеркивается), а произведение 20∙17 заменим равным ему произведением 10∙34. но произведение 10∙34, в свою очередь, можно заменить равным ему произведением 5∙68, поэтому вторая строка вычеркивается: 5∙68=(4+1) ∙68= 4∙68+68 Число 68 запомним (третья строка не вычеркивается), а произведение 4∙68 заменим ему равным произведением 2 ∙136. Но произведение 2∙136 можно заменить ему равным произведением 1∙272, поэтому четвертая строка вычеркивается. Значит, чтобы вычислить произведение 21∙17, нужно сложить 17.68.272 – правые части именно с нечетными множимыми.

Произведения же с четными множимыми всегда можно заменить с помощью раздвоения множимого и удвоения множителя равными им произведениями. Поэтому такие строчки исключаются из вычисления окончательного произведения.

Шло время. В ходу была одновременно чуть ли не дюжина различных способов умножения и деления – приемы один другого запутаннее, твердо запомнить которые не в силах был человек средних способностей.

В книге В.Беллюстина «Как постепенно дошли люди до настоящей арифметики» (1941г.) изложено 27 способов умножения, причем автор отмечает; «весьма возможно, что есть и еще (способы), скрытые в тайниках, книгохранилищах, разбросанные в многочисленных, главным образом, рукописных сборниках».

И все эти приемы умножения – «шахматный», «загибанием», «задом наперед», «алмазом» и прочие, а также все способы деления, носившие не менее затейливые наименования, соперничали друг с другом в громоздкости и сложности.

Во времена М.Ломоносова действие умножения уже записывали почти так, как и в наше время. Только множимое называли «еличество», а произведение - «продукт» и, кроме того, не писали знак умножения.

48 - Еличество. 8 - Множитель. 384 - Продукт, или произведение.

Известно, что М. В. Ломоносов знал наизусть всю «Арифметику» Магницкого. В соответствии с этим учебником маленький Миша Ломоносов умножение 48 на 8 объяснил бы так: «8-жды 8 есть 64, я 4 пишу под чертою, против 8, а 6 десятиц во уме имею. И дальше 8-жды 4 есть 32, и я З во уме держу, а к 2 приложу 6 десятиц, и будет 8. И сие 8 напишу подле 4, в ряд к левой руке, а 3 пока во уме суть, напишу в ряд подле 8, к левой же руке. И будет из умножения 48 с 8 произведение 384».

Сейчас мы почти так же объясняем, только говорим по-современному, а не по-старинному и, кроме того, называем разряды. Например, 3 надо писать на третьем месте потому, что это будут сотни, а не просто «в ряд подле 8, к левой же руке».

Что касается деления… В учебнике Л.Ф.Магницкого дается несколько способов деления. Некоторые из этих способов настолько трудные, что в них очень легко запутаться.

Разберем сейчас один из этих способов. Магницкий считает его изящным и простым.

Пусть требуется разделить 598432 на 678. Сначала пишем первые цифры делимого 5984, под ним делитель 678. Делим 59 на 7 (678 близко к 700), получаем первую цифру частного 8 и пишем ее справа против делимого, умножаем 8 на 678: восемью восемь 64, отнимаем в уме 4 из 4 и пишем над 4 остаток 0; восемью семь 56, да 6 в уме-62, отнимаем 2 от 8, получаем в остатке 6 и пишем его над 8; 8X6=48, 48 +6=54, 59-54=5, значит, над 59 пишем остаток 5. Теперь к остатку 560 сносим следующую цифру делимого 3 и продолжаем действие в таком же порядке.

Закончив с трудом деление, наши предки считали обязательным проверить его один-два раза. Магницкий в данном случае ограничивается одной проверкой. Он рекомендует умножать с высших разрядов: 678 х 8=5424, еще раз. 678 х 8 = 5424 и 678 х 2= 1356; под этими числами подписывает остаток и складывает. Получает делимое. «Верно разделено» - писали в заключение в старину.

Вот как выглядела запись деления:

598432 верно разделено

Как видим, этот способ очень напоминает тот, которым пользуемся мы. Вероятно, наш современный способ развился из этого. Других способов разбирать не будем, приведем только форму записи делений «ромбом», который встречается у Магницкого.

Разделить 9649378 на 5634:

И умножение. Как раз об операции умножения и пойдет речь в этой статье.

Умножение чисел

Умножение чисел осваивается детьми во втором классе, и ничего в этом сложного нет. Сейчас мы рассмотрим умножение на примерах.

Пример 2*5 . Это значит либо 2+2+2+2+2, либо 5+5. Берем 5 два раза или 2 пять раз. Ответ, соответственно, 10.

Пример 4*3 . Аналогично, 4+4+4 или 3+3+3+3. Три раза по 4 или четыре раза по 3. Ответ 12.

Пример 5*3 . Делаем так же как и предыдущие примеры. 5+5+5 или 3+3+3+3+3. Ответ 15.

Формулы умножения

Умножение – это сумма одинаковых чисел, например, 2 * 5 = 2 + 2 + 2 + 2 + 2 или 2 * 5 = 5 + 5. Формула умножения:

Где, а – любое число, n – число слагаемых а. Допустим, а=2, тогда 2+2+2=6, тогда n=3 умножая 3 на 2, получаем 6.Рассмотрим в обратном порядке. Например, дано: 3 * 3, то есть. 3 умножить на 3 – это значит, что тройку надо взять 3 раза: 3 + 3 + 3 = 9. 3 * 3=9.

Сокращенное умножение

Сокращенное умножение – сокращение операции умножения в определенных случаях, и специально для этого выведены формулы сокращенного умножения. Которые помогут сделать вычисления наиболее рациональными и быстрыми:

Формулы сокращенного умножения

Пусть a, b принадлежат R, тогда:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения. Формула: (a+b)^2 = a^2 + 2ab + b^2

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения. Формула: (a-b)^2 = a^2 - 2ab + b^2

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы. Формула: a^2 - b^2 = (a - b)(a + b)

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения. Формула: (a + b)^3 = a^3 + 3a(^2)b + 3ab^2 + b^3

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения. Формула: (a-b)^3 = a^3 - 3a(^2)b + 3ab^2 - b^3

Сумма кубов a^3 + b^3 = (a + b)(a^2 - ab + b^2)

Разность кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений. Формула: a^3 - b^3 = (a - b)(a^2 + ab + b^2)

Запишитесь на курс "Ускоряем устный счет, НЕ ментальная арифметика", чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Умножение дробей

Рассматривая сложение и вычитание дробей, прозвучало правило, приведения дробей к общему знаменателю, чтобы выполнить расчет. При умножении этого делать не надо ! При умножении двух дробей, умножается знаменатель на знаменатель, а числитель на числитель.

Например, (2/5) * (3 * 4). Умножим две трети на одну четверть. Умножаем знаменатель на знаменатель, а числитель на числитель: (2 * 3)/(5 * 4), тогда 6/20, совершаем сокращение, получаем 3/10.

Умножение 2 класс

Второй класс – это только начала изучения умножения, поэтому второклассники решают простейшие задачки на замену сложения умножением, умножают числа, учат таблицу умножения.Давайте рассмотрим задачи на умножение уровня второго класса:

Олег живет в пяти этажном доме, на самом верхнем этаже. Высота одного этажа равняется 2 метрам. Какова высота дома?

В коробке находятся 10 упаковок с печеньем. В каждой упаковке их 7 штук. Сколько печенья в коробке?

Миша расставил свои игрушечные машинки в ряд. В каждом ряду их 7, а рядов всего 8. Сколько у Миши машинок?

В столовой стоят 6 столов, а за каждым столом задвинуты 5 стульев. Сколько стульев в столовой?

Мама с магазина принесла 3 пакета с апельсинами. В пакетах находятся по 22 апельсина. Сколько апельсиновпринесла мама?

В саду растет 9 кустов клубники, а на каждом кустике растет 11 ягод. Сколько ягод растет на всех кустиках?

Рома положил друг за другом 8 деталей трубы, одинакового размера по 2 метра. Какова длина полной трубы?

В школу родители на первое сентября привезли детей. Приехало 12 машин, в каждой было по 2 ребенка. Сколькодетей привезли родители на этих машинах?

Умножение 3 класс

В третьем классе даются уже более серьезные задания. Помимо умножения будет так же проходиться Деление .

Среди заданий на умножение будет: умножение двузначных чисел, умножение столбиком, замена сложения умножением и наоборот.

Умножение столбиком:

Умножение столбиком – самый простой способ перемножить большие числа. Рассмотрим данный метод на примередвух чисел 427 * 36.

1 шаг . Запишем числа друг под другом, так чтобы 427 было на верху, а 36 внизу, то есть 6 под 7, 3 под 2.

2 шаг . Умножение начинаем с крайней правой цифры нижнего числа. То есть порядок умножения таков: 6 * 7, 6 * 2, 6 * 4, затем так же с тройкой: 3 * 7, 3 * 2, 3 * 4.

Итак, умножаем сначала 6 на 7, ответ:42. Записываем так: так как получилось 42, то 4 – десятки, а 2 – единицы, запись происходит аналогично сложению, а значит 2 записываем под шестеркой, а 4 прибавляем к двойке числа 427.

3 шаг . Затем аналогично делаем с 6 * 2. Ответ: 12. Первый десяток, который прибавляется к четверке числа 427, а второй – единицы. Складываем полученную двойку с четверкой от предыдущего умножения.

4 шаг . Умножаем 6 на 4. Ответа 24 и прибавляем 1 от предыдущего умножения. Получаем 25.

Итак, умножив 427 на 6, получился ответ 2562

ЗАПОМНИТЕ! Результат второго умножения нужно начать записывать под ВТОРОЙ цифрой первого результата!

5 шаг . Совершаем аналогичные действия с цифрой 3. Получаем ответ умножения 427 * 3=1281

6 шаг . Затем полученные ответы при умножении складываем и получаем итоговый ответ умножения 427 * 36. Ответ: 15372.

Умножение 4 класс

Четвертый класс – это уже умножение только больших чисел. Вычисление выполняются методом умножения в столбик. Метод описан выше доступным языком.

Например, найти произведение следующих пар чисел:

1. 988 * 98 =
2. 99 * 114 =
3. 17 * 174 =
4. 164 * 19 =

Презентация на умножение

Скачайте презентацию на умножение с простейшими заданиями для второклассников. Презентация поможет детям лучше ориентироваться в этой операции, потому что она составлена красочно и в игровом стиле – в лучшем варианте для обучения ребенка!

Таблица умножения

Таблица умножения учится каждым школьником во втором классе. Ее обязан знать каждый!

Запишитесь на курс "Ускоряем устный счет, НЕ ментальная арифметика", чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Примеры на умножение

Умножение на однозначное

1. 9 * 5 =
2. 9 * 8 =
3. 8 * 4 =
4. 3 * 9 =
5. 7 * 4 =
6. 9 * 5 =
7. 8 * 8 =
8. 6 * 9 =
9. 6 * 7 =
10. 9 * 2 =
11. 8 * 5 =
12. 3 * 6 =

Умножение на двузначное

1. 4 * 16 =
2. 11 * 6 =
3. 24 * 3 =
4. 9 * 19 =
5. 16 * 8 =
6. 27 * 5 =
7. 4 * 31 =
8. 17 * 5 =
9. 28 * 2 =
10. 12 * 9 =

Умножение двузначное на двузначное

1. 24 * 16 =
2. 14 * 17 =
3. 19 * 31 =
4. 18 * 18 =
5. 10 * 15 =
6. 15 * 40 =
7. 31 * 27 =
8. 23 * 25 =
9. 17 * 13 =

Умножение трехзначных чисел

1. 630 * 50 =
2. 123 * 8 =
3. 201 * 18 =
4. 282 * 72 =
5. 96 * 660 =
6. 910 * 7 =
7. 428 * 37 =
8. 920 * 14 =

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра "Быстрый счет"

Игра «быстрый счет» поможет вам усовершенствовать свое мышление . Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.

Игра "Математические матрицы"

«Математические матрицы» великолепное упражнение для мозга детей , которое поможет вам развить его мыслительную работу, устный счет, быстрый поиск нужных компонентов, внимательность. Суть игры заключается в том, что игроку предстоит из предложенных 16 чисел найти такую пару, которая в сумме даст данное число, например на картинке ниже данное число «29», а искомая пара «5» и «24».

Игра "Числовой охват"

Игра «числовой охват» нагрузит вашу память во время занятий с данным упражнением.

Суть игры – запомнить цифру, на запоминание которой отводится около трех секунд. Затем нужно ее воспроизвести. По мере прохождения этапов игры, количество цифр растет, начинаете с двух и далее.

Игра "Угадай операцию"

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра "Упрощение"

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра "Быстрое сложение"

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра "Визуальная геометрия"

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра "Математические сравнения"

Игра «Математические сравнения» развивает мышление и память. Главная суть игры сравнить числа и математические операции. В этой игре надо сравнить два числа. На верху, написан вопрос, прочитайте его и ответьте правильно на поставленный вопрос. Ответить можно при помощи кнопок расположенных внизу. Там нарисованы три кнопки «левое», «равно» и «правое». Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше - записывайтесь на наш курс: Ускоряем устный счет.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

перемножить в любом порядке.

Методически данное правило имеет целью подготовить ребенка к знакомству со способами умножения в столбик чисел, оканчиваю­щихся нулями, поэтому с ним знакомятся только в четвертом клас­се. Реально данное свойство умножения позволяет рационализи­ровать устные вычисления как во 2, так и в 3 классе.

Например:

Вычисли: (7 2) 5 = ...

В данном случае намного легче вычислить вариант

7 (2 5) = 7 10 - 70.

Вычисли: 12 (5 7) = ...

8 данном случае намного легче вычислить вариант (12-5)-7 = 60-7 = 420.

Приемы вычислений

1. Умножение и деление чисел, оканчивающихся нулем: 20 3; 3 20; 60: 3; 80: 20

Вычислительный прием в данном случае сводится к умноже­нию и делению однозначных чисел, выражающих число десятков в заданных числах. Например:

20 3 =... 3 20 =... 60:3 = ...

2 дес. 3 = 20 3 = 60 б дес.: 3 = 2 дес.

20 - 3 = 60 3 20 = 60 60: 3 = 20

Для случая 80:20 может быть использовано два способа вычис­лений: тот, что использовался в предыдущих случаях, и способ под­бора частного.

Например: 80: 20 =... 80: 20 =...

8 дес.: 2 дес. = 4 или 20 4 = 80

80: 20 = 4 80: 20 = 4

В первом случае использовался прием представления двузнач­ных десятков в виде разрядных единиц, что сводит рассматривае­мый случай к табличному (8:2). Во втором случае цифра частного находится подбором и проверяется умножением. Во втором случае ребенок возможно не сразу подберет верную цифру частного, это означает, что проверка будет выполнена не один раз.

2. Прием умножения двузначного числа на однозначное: 23 4; 4-23

При умножении двузначного числа на однозначное актуализи­руются следующие знания и умения:

В случае умножения вида 4 23 сначала применяется переста­новка множителей, а затем та же схема умножения, что и выше.

3. Прием деления двузначного числа на однозначное: 48:3; 48:2

При делении двузначного числа на однозначное актуализиру­ются следующие знания и умения:

4. Прием деления двузначного числа на двузначное: 68: 17

При делении двузначного числа на двузначное необходимы сле­дующие знания и умения:

Сложность последнего приема состоит в том, что ребенок не может сразу подобрать нужную цифру частного и выполняет несколько прове­рок подобранных цифр, что требует достаточно сложных вычислений. Многие дети тратят много времени на выполнение вычислений этого вида, поскольку начинают не столько подбирать подходящую цифру частного, сколько перебирают все множители подряд, начиная с двух.

С целью облегчения вычислений могут быть использованы два приема:

1) ориентировка на последнюю цифру делимого;

2) прием округления.

Первый прием предполагает, что при подборе возможной циф­ры частного ребенок ориентируется на знание таблицы умноже­ния, сразу перемножая подобранную цифру (число) и последнюю цифру делителя.

Например, 3-7 = 21. Последняя цифра числа 68 - это 8, значит нет смысла умножать 17 на 3, последняя цифра делителя все равно не сов­падает. Пробуем в частном число 4 - умножаем 7 4 = 28. Последняя цифра совпадает, значит имеет смысл найти произведение 17 4.

Второй прием предполагает округление делителя и подбор циф­ры частного с ориентиром на округленный делитель.

Например, 68:17 делитель 17 округляется до 20. Примерная циф­ра частного 3 дает при проверке 20 3 = 60 < 68, значит имеет смысл сразу проверять в качестве цифры частного 4:17 4 = 68.

Эти приемы позволяют сократить затраты сил и времени при выполнении вычислений данного вида, но требуют хорошего зна­ния таблицы умножения и умения округлять числа.

Целые числа, оканчивающиеся цифрами 0,1,2,3,4, округляют до ближайшего целого десятка, отбрасы­вая эти цифры.

Например, числа 12, 13, 14 следует округлять до 10. Числа 62, 63, 64 округляют до 60.

Целые числа, оканчивающиеся цифрами 5, 6, 7,8,9, округляют до ближайшего целого десятка в большую сторону.

Например, числа 15,16,17,18,19 округляют до 20. Числа 45,47, 49 округляют до 50.

Порядок действий в выражениях, содержащих умножение и деление

Правила порядка выполнения действий задают основные при­знаки выражений, на которые следует ориентироваться при вычис­лении их значений.

Первые правила, определяющие порядок действий в арифме­тических выражениях, задавали порядок действий в выражениях, содержащих действия сложения и вычитания:

1. В выражениях без скобок, содержащих только действия сложения и вычитания, действия выполня­ются в том порядке, как они записаны: слева направо.

2. Действия в скобках выполняют первыми.

3. Если выражение содержит только действия сло­жения, то два соседних слагаемых всегда можно заме­нить их суммой (сочетательное свойство сложения).

В 3 классе изучаются новые правила порядка выполнения дей­ствий в выражениях, содержащих умножение и деление:

4. В выражениях без скобок, содержащих только умножение и деление, действия выполняются в том порядке, как они записаны: слева направо.

5. В выражениях без скобок умножение и деление выполняются раньше, чем сложение и вычитание.

При этом установка на выполнение действия в скобках первым сохраняется. Возможные случаи нарушения этой установки были оговорены ранее.

Правила порядка выполнения действий являются общими пра­вилами вычислений значений математических выражений (при­меров), которые сохраняются на протяжении всего периода изучения математики в школе. В связи с этим формирование у ре­бенка четкого понимания алгоритма порядка выполнения дейст­вий является важной преемственной задачей обучения математике в начальной школе. Проблема заключается в том, что правила по­рядка выполнения действий являются достаточно вариативными и не всегда однозначно заданными.

Например, в выражении 48-3 + 7 + 8 следует по общей уста­новке применять правило 1 для выражения без скобок, содержа­щего действия сложения и вычитания. В то же время, как вариант рациональных вычислений, можно использовать прием замены суммой части 7 + 8, поскольку после вычитания числа 3 из 48 по­лучится 45, к чему удобно прибавить 15.

Однако подобный разбор такого выражения в начальных клас­сах не предусмотрен, поскольку есть опасения, что при неадекват­ном понимании такого подхода ребенок будет применять его в случаях вида 72 - 9 - 3 + 6. В данном случае замена выражения 3 + 6 суммой невозможна, она приведет к неверному ответу.

Большая вариативность в применении всей группы правил и вариантов правил при определении порядка действий требует значительной гибкости мышления, хорошего понимания смысла математических действий, последовательности мыслительных дей­ствий, математического «чутья» и интуиции (математики называ­ют это «чувство числа»). Реально намного проще приучить ребенка жестко соблюдать четко установленный порядок анализа число­вого выражения с точки зрения тех признаков, на которые ориен­тировано каждое правило.

Определяя порядок действий, рассуждай так:

1) Если есть скобки, выполняю первым действие, за­писанное в скобках.

2) Выполняю по порядку умножение и деление.

3) Выполняю по порядку сложение и вычитание.

Данный алгоритм задает порядок действий достаточно одно­значно, хотя и с небольшими вариациями.

В этих выражениях порядок действии определен алгоритмом однозначно и является единственно возможным. Приведем другие примеры

После выполнения умножения и деления в данном примере можно было сразу к 54 прибавить 6, а из 18 вычесть 9, пбсле чего результаты сложить. Технически было бы значительно легче, чем путь, обусловленный алгоритмом, возможен изначально другой по­рядок действий в примере:

Таким образом, вопрос о формировании умения определять по­рядок действий в выражениях в начальной школе определенным образом противоречит необходимости обучать ребенка способам рациональных вычислений.

Например, в случае порядок действий определен алгоритмом абсолютно однозначно, при этом требует отребенка сложнейших вычислений в уме с переходами через разряд: 42 - 7 и 35 + 8.

Если же после выполнения деления 21:3, выполнить сложение 42 + 8 = 50, а затем вычитание 50 - 7 = 43, что намного легче тех­нически, ответ будет тот же. Этот путь вычислений противоречит установке данного в учебнике

При умножении и делении целых чисел применяется несколько правил. В данном уроке мы рассмотрим каждое из них.

При умножении и делении целых чисел следует обращать внимание на знаки чисел. От них будет зависеть какое правило применять. Также, необходимо изучить несколько законов умножения и деления. Изучение этих правил позволяет избежать некоторые досадные ошибки в будущем.

Содержание урока

Законы умножения

Некоторые из законов математики мы рассматривали в уроке . Но мы рассмотрели не все законы. В математике немало законов, и разумнее будет изучать их последовательно по мере необходимости.

Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого , множителя и произведения . Например, в выражении 3 × 2 = 6 , число 3 — это множимое, число 2 — множитель, число 6 — произведение.

Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.

Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.

Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.

Выражение 3 × 2 также можно понимать, как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:

Таким образом, если число 3 повторить два раза подряд, получится число 6.

Переместительный закон умножения

Множимое и множитель называют одним общим словом – сомножители . Переместительный закон умножения выглядит следующим образом:

От перестановки мест сомножителей произведение не меняется.

Проверим так ли это. Умножим к примеру 3 на 5. Здесь 3 и 5 это сомножители.

3 × 5 = 15

Теперь поменяем местами сомножители:

5 × 3 = 15

В обоих случаях, мы получаем ответ 15, значит между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:

3 × 5 = 5 × 3

15 = 15

А с помощью переменных переместительный закон умножения можно записать так:

a × b = b × a

где a и b — сомножители

Сочетательный закон умножения

Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.

К примеру выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:

3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24

Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:

3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24

В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:

(3 × 2) × 4 = 3 × (2 × 4)

а с помощью переменных сочетательный закон умножения можно записать так:

a × b × c = (a × b) × c = a × (b × c)

где вместо a, b, c могут стоять любые числа.

Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.

Например, найдём значение выражения (2 + 3) × 5

Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:

(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25

Значит значение выражения (2 + 3) × 5 равно 25 .

С помощью переменных распределительный закон умножения записывается так:

(a + b) × c = a × c + b × c

где вместо a, b, c могут стоять любые числа.

Закон умножения на ноль

Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.

Произведение равно нулю, если хотя бы один из сомножителей равен нулю.

Например, выражение 0 × 2 равно нулю

В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза» . Но как можно увеличить ноль в два раза, если это ноль? Ответ — никак.

Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».

И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:

Примеры применения закона умножения на ноль:

5 × 5 × 5 × 0 = 0

2 × 5 × 0 × 9 × 1 = 0

В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.

Мы рассмотрели основные законы умножения. Далее рассмотрим умножение целых чисел.

Умножение целых чисел

Пример 1. Найти значение выражения −5 × 2

Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. Для таких случаев нужно применять следующее правило:

Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.

−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10

Обычно записывают короче: −5 × 2 = −10

Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.

Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить двойку. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:

То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы

А выражение (−5) + (−5) равно −10. Мы это знаем из . Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.

Пример 2. Найти значение выражения 12 × (−5)

Это умножение чисел с разными знаками. 12 – положительное число, (−5) – отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:

12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60

Обычно решение записывают покороче:

12 × (−5) = −60

Пример 3. Найти значение выражения 10 × (−4) × 2

Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:

Первое действие:

10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40

Второе действие:

−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80

Значит значение выражения 10 × (−4) × 2 равно −80

Запишем решение покороче:

10 × (−4) × 2 = −40 × 2 = −80

Пример 4. Найти значение выражения (−4) × (−2)

Это умножение отрицательных чисел. В таких случаях нужно применять следующее правило:

Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс

(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8

Плюс по традиции не записываем, поэтому просто записываем ответ 8.

Запишем решение покороче (−4) × (−2) = 8

Возникает вопрос почему при умножении отрицательных чисел вдруг получается положительное число. Давайте попробуем доказать, что (−4) × (−2) равно 8 и ни чему другому.

Сначала запишем следующее выражение:

Заключим его в скобки:

(4 × (−2) )

Прибавим к этому выражению наше выражение (−4) × (−2). Его тоже заключим в скобки:

(4 × (−2) ) + ((−4) × (−2) )

Всё это приравняем к нулю:

(4 × (−2)) + ((−4) × (−2)) = 0

Теперь начинается самое интересное. Суть в том, что мы должны вычислить левую часть этого выражения, и в результате получить 0.

Итак, первое произведение (4 × (−2)) равно −8. Запишем в нашем выражении число −8 вместо произведения (4 × (−2))

−8 + ((−4) × (−2)) = 0

Теперь вместо второго произведения временно поставим многоточие

Теперь внимательно посмотрим на выражение −8 + … = 0. Какое число должно стоять вместо многоточия, чтобы соблюдалось равенство? Ответ напрашивается сам. Вместо многоточия должно стоять положительное число 8 и никакое другое. Только так будет соблюдаться равенство. Ведь −8 + 8 равно 0.

Возвращаемся к выражению −8 + ((−4) × (−2)) = 0 и вместо произведения ((−4) × (−2)) записываем число 8

Пример 5. Найти значение выражения −2 × (6 + 4)

Применим распределительный закон умножения, то есть умножим число −2 на каждое слагаемое суммы (6 + 4)

−2 × (6 + 4) = −2 × 6 + (−2) × 4

Теперь выполним умножение, и сложим полученные результаты. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение

Первое действие:

−2 × 6 = −12

Второе действие:

−2 × 4 = −8

Третье действие:

−12 + (−8) = −20

Значит значение выражения −2 × (6 + 4) равно −20

Запишем решение покороче:

−2 × (6 + 4) = (−12) + (−8) = −20

Пример 6. Найти значение выражения (−2) × (−3) × (−4)

Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение

Первое действие:

(−2) × (−3) = 6

Второе действие:

6 × (−4) = −(6 × 4) = −24

Значит значение выражения (−2) × (−3) × (−4) равно −24

Запишем решение покороче:

(−2) × (−3) × (−4) = 6 × (−4) = −24

Законы деления

Прежде чем делить целые числа, необходимо изучить два закона деления.

В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого , делителя и частного . Например, в выражении 8: 2 = 4, 8 – это делимое, 2 – делитель, 4 – частное.

Делимое показывает, что именно мы делим. В нашем примере мы делим число 8.

Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть в ходе операции деления, число 8 будет разделено на две части.

Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2.

На ноль делить нельзя

Любое число запрещено делить на ноль.

Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10: 5 = 2.

Видно, что второе выражение записано в обратном порядке. Если к примеру, у нас имеется два яблока и мы захотим увеличить их в пять раз, то мы запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то мы запишем 10: 5 = 2

Точно так же можно поступать и с другими выражениями. Если к примеру, 2 × 6 = 12, то мы можем обратно вернуться к изначальному числу 2. Для этого достаточно записать выражение 2 × 6 = 12 в обратном порядке, разделяя 12 на 6

Теперь рассмотрим выражение 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю

Если записать это выражение в обратном порядке, то получим:

Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно.

В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0

В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.

Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое.

Например выражение 8: 2 означает найти такое число, которое при умножении на 2 даст 8

Здесь вместо многоточия должно стоять число, которое при умножении на 2 даст ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке:

Получили число 4. Запишем его вместо многоточия:

Теперь представим, что нужно найти значение выражения 5: 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5

Здесь вместо многоточия должно стоять число, которое при умножении на 0 даст ответ 5. Но не существует числа, которое при умножении на ноль даёт 5.

Выражение … × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю.

А значит записывать выражение … × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя.

С помощью переменных данный закон записывается следующим образом:

При b ≠ 0

Число a можно разделить на число b , при условии, что b не равно нулю.

Свойство частного

Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится.

Например, рассмотрим выражение 12: 4. Значение этого выражения равно 3

Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3

(12 × 4 ) : (4 × 4 )

(12 × 4 ) : (4 × 4 ) = 48: 16 = 3

Получили ответ 3.

Теперь попробуем не умножить, а разделить делимое и делитель на число 4

(12: 4 ) : (4: 4 )

(12: 4 ) : (4: 4 ) = 3: 1 = 3

Получили ответ 3.

Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется.

Деление целых чисел

Пример 1. Найти значение выражения 12: (−2)

Это деление чисел с разными знаками. 12 — положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус.

12: (−2) = −(|12| : |−2|) = −(12: 2) = −(6) = −6

Обычно записывают покороче:

12: (−2) = −6

Пример 2. Найти значение выражения −24: 6

Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. Опять же модуль делимого делим на модуль делителя, и перед полученным ответом ставим минус.

−24: 6 = −(|−24| : |6|) = −(24: 6) = −(4) = −4

Запишем решение покороче:

Пример 3. Найти значение выражения −45: (−5)

Это деление отрицательных чисел. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.

−45: (−5) = |−45| : |−5| = 45: 5 = 9

Запишем решение покороче:

−45: (−5) = 9

Пример 4. Найти значение выражения −36: (−4) : (−3)

Согласно , если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.

Разделим −36 на (−4), и полученное число разделим на −3

Первое действие:

−36: (−4) = |−36| : |−4| = 36: 4 = 9

Второе действие:

9: (−3) = −(|9| : |−3|) = −(9: 3) = −(3) = −3

Запишем решение покороче:

−36: (−4) : (−3) = 9: (−3) = −3

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках