Электростатическое поле заряженной оси

Электростатическое поле заряженной оси

Заряженной осью называется очень тонкий, теоретически бесконечно длинный проводник, несущий на себе заряд. Весь заряд оси указать невозможно (он равен бесконечности), поэтому указывается линейный заряд

, т.е. заряд, приходящийся на единицу длины оси. Пусть ось с положительным зарядом τ находится в среде с проницаемостью ε а (рис.11.15). Используя интегральную форму теоремы Гаусса, произведем расчет напряженности поля в произвольной точке, удаленной на расстояние r от оси. С этой целью проведем через данную точку замкнутую поверхность в виде цилиндра длиной l . Поток вектора Е имеет место только через боковую поверхность этого цилиндра, поскольку в точках, расположенных на его донышках векторы Е и ds перпендикулярны и их произведение равно нулю. В точках же боковой поверхности векторы Е и ds совпадают по направлению и их произведение равно произведению модулей, а модуль Е одинаков во всех этих точках в силу симметрии. С учетом сказанного имеем Внутри поверхности интегрирования заряд

. Поэтому

или

т.е. напряженность в данном поле изменяется обратно пропорционально расстоянию от оси.

Потенциал Постоянная интегрирования А зависит от того, где расположить точку с нулевым потенциалом. Следовательно, в данном поле потенциал изменяется по логарифмическому закону.

Электростатическое поле двух заряженных осей

На практике чаще всего две заряженные оси несут на себе равные по величине и противоположные по знаку заряды +E ds l r τ и -τ . Именно такой случай и рассмотрим (рис.11.16). Возьмем в поле произвольную точку М , положение которой будем характеризовать расстоянием а до положительной оси и расстоянием b до отрицательной оси и в первую очередь рассчитаем в ней напряженность поля, используя метод наложения:

где

- составляющие, создаваемые положительно и отрицательно заряженной осью соответственно. Величины этих составляющих могут быть определены по формулам, взятым из предыдущей темы, а именно:

Аналогично для потенциала

, где . Тогда Из последнего выражения следует, что совокупность точек, для которых

, представляет собой эквипотенциаль. Из геометрии известно, что геометрическим местом точек, отношение расстояний от которых до двух заданных точек является величиной постоянной, есть окружность (теорема Аполлония). Поэтому эквипотенциали в поле двух заряженных осей являются окружностями. Для построения эквипотенциальной линии, проходящей через точку М , проводим биссектрисы внутреннего аМ b н внешнего рМа углов. Точки пересечения этих биссектрис с линией, проведенной через оси, (т.1 и т.2), а также т. М являются тремя точками этой эквипотенциали. Центр этой окружности находится в точке, расположенной посредине между т.1 и т.2.

Электростатическое поле и ёмкость двухпроводной линии электропередачи (ЛЭП)

Пусть провода ЛЭП имеют одинаковый радиус r о , расположены на расстоянии d друг от друга и находятся в среде с проницаемостью ε а (рис.11.17). Если левому проводу сообщен заряд τ на единицу длины, правому -τ , то в пространстве между проводами возникнет электростатическое поле, которое можно представить в виде части поля двух заряденных осей. Действительно, поскольку провода металлические, то внутри них поля нет (Е =0), а потенциал всех точек каждого провода одинаков, т.е. поверхность каждого провода является эквипотенциальной. Поэтому две заряженные оси, расположенные в т. m и n, создадут такую же картину поля как и двухпроводная ЛЭП, если т. m и n расположить так, чтобы поверхности проводов были для них эквипотенциалями. Точки m и n принято называть электрическими осями в отличие от геометрических осей (точки О и О 1). Смещение электрических и геометрических осей (x ) в силу симметрии одинаково в левом и правом проводе. Для определения величины x возьмём точки 1 и 2 и запишем выражения потенциалов этих точек в поле двух заряженных осей, расположенных в т. m и n .

Так как т. 1 и 2 расположены на поверхности одного и того же провода, то φ 1 =φ 2 , следовательно,

Решая это равенство относительно x , получим

В этом выражении при отсчете x от т.О плюс определяет положение т. n , а минус – положение т. m . Если d>>r o , то x 1 =0, x 2 =d , т.е. электрические и геометрические оси совпадают (нет смещения осей). Часто x не вычисляют по полученной выше формуле, а получают графическим путем. Для этого проводят общую касательную к поверхности проводников, делят расстояние между точками касания (P и Q) пополам (т. С) и проводят дугу окружности, проходящей через т. Р и Q и имеющей центр в т. С. Точки пересечения этой окружности с линией О 1 О дают положение электрических осей. Из геометрического определения положения электрических осей так же видно, что при d>>r o т. m и n сольются с т. О и О 1 .

После того, как определено смещение осей, задача сведена к предыдущей.

Перейдем к вопросу о ёмкости двухпроводной линии. Если два проводника разделены диэлектриком и несут на себе равные по величине и противоположные по знаку заряды, то в пространстве между ними создается электростатическое поле. Пусть напряжение между проводниками равно U . Тогда ёмкостью между проводниками называется отношение абсолютной величины заряда на одном из тел к напряжению между ними:

. Единица измерения ёмкости – Фарада (

). Так как напряжение между телами пропорционально заряду на них, то ёмкость ни от заряда, ни от напряжения не зависит, а зависит она от конфигурации и геометрических размеров тел, их взаимного расположения и от свойств диэлектрика, в котором они находятся. Существуют устройства, предназначенные для получения определенной величины ёмкости – это конденсаторы, однако ёмкостью обладают не только конденсаторы, а всякие два тела, способные нести на себе равные по величине и противоположные по знаку заряды.

Определим ёмкость двухпроводной линии. Напряжение между проводами Заряд одного из проводов q=τl . Тогда

Часто определяют ёмкость единицы длины линии

А если d>>r o , то x =0 и

Из полученных формул видно, что ёмкость действительно зависит от размеров линии и свойств среды, в которой находятся провода, в частности, если увеличивать расстояние d между проводами, то ёмкость будет уменьшаться.

Электростатическое поле и ёмкость коаксиального кабеля

Коаксиальный кабель представляет собой два металлических соосных цилиндра, расположенных один внутри другого и изолированных друг от друга диэлектриком с проницаемостью ε а (рис.11.18). Такой кабель широко применяется на высоких частотах. Пусть внутренний цилиндр, который называется жилой, несёт на себе заряд +τ , а наружный цилиндр (оболочка) – заряд –τ . Тогда возникнет электростатическое поле, расчёт которого произведём для отдельных областей кабеля. Внутри жилы (0>r>r 1) поля нет, так как жила проводящая, т.е. E =0, φ =const. Для определения напряжённости поля в пространстве между жилой и оболочкой воспользуемся теоремой Гаусса:

В качестве поверхности интегрирования возьмём цилиндр радиуса r и длиной l . Поток вектора Е через донышки этого цилиндра равен нулю (векторы Е и ds перпендикулярны), а через его боковую поверхность



Тогда

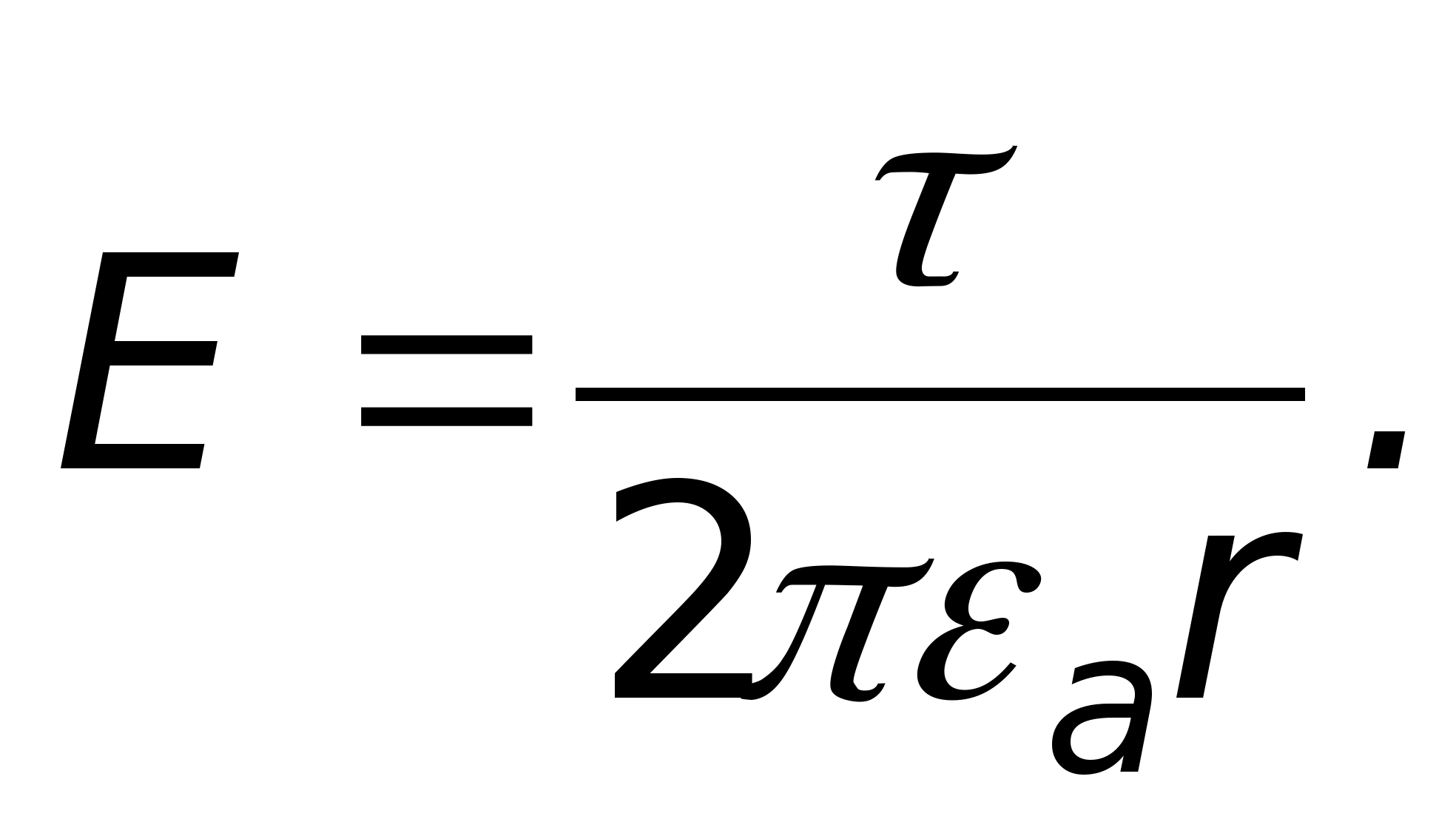Так как Е имеет только радиальную составляющую, то

Для всех точек оболочки кабеля (r 2 3) E =0, φ =const, так как она проводящая. За пределами кабеля (r 3 поэтому E =0, φ =const. Таким образом в данном устройстве поле имеется только в пространстве между жилой и оболочкой.

Ёмкость коаксиального кабеля С = где q=τl , a

Тогда

, а

Электростатическое поле и ёмкость однослойного и двухслойного плоских конденсаторов

Однослойный плоский конденсатор состоит из двух металлических пластин сечением S , расположенных на расстоянии d друг от друга (рис.11.19). Определим закон изменения Е , D и φ , если к нему подведено напряжение U . Если размеры пластин (длина, высота) намного больше d, то можно пренебречь краевым эффектом (искажением поля на краях пластин) и считать его электростатическое поле равномерным, т.е. при всех значениях х напряженность поля одна и та же. Тогда

откуда

а D =ε a E=

Так как

а φ зависит только от х (плоскость yoz - эквипотенциаль), то

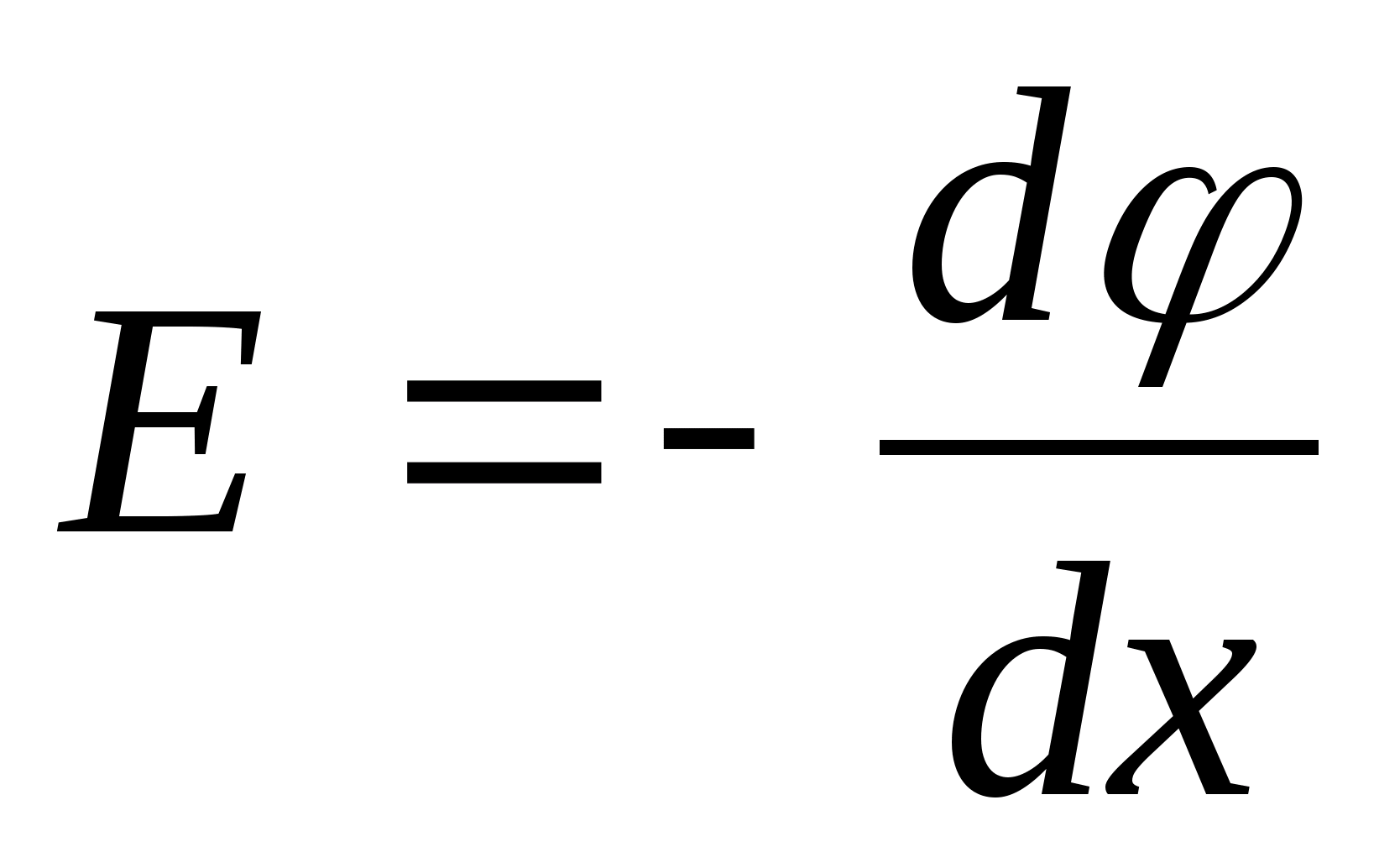или

Для определения постоянной интегрирования А примем, что потенциал правой пластины равен нулю, а левой равен U , т.е. при х =0 φ= U . Тогда А= U и

т.е. φ изменяется по линейному закону в зависимости от х .

Определим ёмкость плоского конденсатора С = где U=Ed. Для определения заряда, например, левой пластины воспользуемся теоремой Гаусса:

причем

Определим поток вектора D через замкнутую поверхность, охватывающую эту пластину (рис.11.19)

так как векторы D и ds совпадают по направлению и D имеет одно и тоже значение во всех точках, находящихся внутри конденсатора. Следовательно, q=DS= ε a ES и

Двухслойный конденсатор (рис.11.20) отличается от предыдущего тем, что изоляция между пластинами состоит из двух слоёв с проницаемостями ε 1а и ε 2а. Если по-прежнему пренебречь краевым эффектом, то поле такого конденсатора характерно тем, что в каждом слое оно является однородным с напряженностями Е 1 и Е 2 соответственно. Тогда

Однако этого уравнения недостаточно для определения Е 1 и Е 2 . Для составления второго уравнения используем граничные условия. Известно, что на границе раздела двух разных диэлектриков равны нормальные составляющие вектора электростатической индукции (D 1 n =D 2 n ). Если учесть, что в нашем случае эти векторы перпендикулярны к границе, то это равенство примет вид D 1 =D 2 или ε 1 а Е 1 = ε 2 а Е 2 . Это и будет второе уравнение. Решая совместно эти уравнения, получим

Определим закон изменения потенциала:

Постоянную интегрирования А 1 определим из условия, что при х =0 φ 1 = U (А 1 =U ), а А 2 – из условия, что при х =d 1 φ 1 =φ 2 (или φ 2 =0 при х =d 1 +d 2). Из полученных формул видно, что потенциал изменяется по линейному закону. На рис.11.21 показаны графики зависимости от х индукций, напряженностей и потенциалов.

Ёмкость такого конденсатора определяется как эквивалентная двух последовательно соединенных ёмкостей:

где

ёмкость первого слоя, а

ёмкость второго слоя изоляции конденсатора.

Метод зеркальных изображений

Данный метод применяется для расчета полей, в которых имеется геометрически правильной формы граница раздела различных сред. Это искусственный расчетный метод, сущность которого заключается в том, что в расчет кроме заданных зарядов вводятся еще дополнительные или фиктивные заряды, величина и место расположения которых выбираются такими, чтобы выполнялись граничные условия. Чаще всего фиктивные заряды располагаются в точках зеркального изображения по отношению к заданным, отсюда и название метода. Дополнительные или фиктивные заряды в расчет вводятся для того, чтобы учесть влияние появляющихся в результате электростатической индукции свободные или связанные заряды.

Поле заряженной оси, расположенной вблизи проводящей поверхности

Пусть заряженная ось с зарядом  расположена параллельно поверхности проводящей среды (рис.11.22). Этой проводящей средой может быть металлическая плита или стенка дома, но чаще всего это земля. Вследствие электростатической индукции на поверхности проводящего тела наводятся заряды, наличие которых приводит к искажению поля по сравнению с полем уединенной оси. Распределение индуктированных зарядов по поверхности проводящей среды является весьма сложным и неизвестным. Несмотря на это задача расчета поля в верхнем полупространстве, заполненном диэлектриком с проницаемостью  а (в нижнем полупространстве поля нет поскольку там проводящая среда), может быть достаточно просто решена методом зеркальных изображений. Поместим в точку, являющуюся зеркальным изображением заданной оси относительно проводящей поверхности, фиктивную ось с зарядом такой же величины, но противоположного знака, т.е. - (заметим, что так будет не всегда, фиктивный заряд может иметь и другие величины и знак). Убедимся в том, что напряженность Е от двух заряженных осей ( и - ) в любой точке границы раздела сред не имеет тангенциальной составляющей. Действительно, так как тангенциальные составляющие от обоих зарядов имеют противоположные направления и в сумме дают ноль. Следовательно, граничные условия между диэлектриком и проводником выполняются, что доказывает правильность выбора величины и места расположения фиктивного заряда. Поэтому напряженность поля и потенциал в любой точке диэлектрика можно определять по известным формулам поля двух заряженных осей: где а – расстояние до положительно заряженной оси, b – расстояние до отрицательно заряженной оси. Если бы фактическая ось несла на себе заряд - , то задача решалась бы аналогично, только фиктивная ось имела бы заряд + . Аналогично решается задача о поле точечного заряда, расположенного вблизи проводящей среды.

Электростатическое поле системы проводников, расположенных вблизи проводящей поверхности (частичные ёмкости)

В качестве системы проводников, расположенных вблизи проводящей поверхности, рассмотрим многопроводную линию электропередачи (ЛЭП), состоящую из n весьма длинных проводов, протянутых параллельно поверхности земли (рис.11.23).

Пусть известны заряды каждого провода  к (будем считать их положительными), их радиусы r к, высоты подвеса h к, взаимное расположение и свойства среды ( а ), в которой они находятся. Вследствие электростатической индукции на поверхности земли появятся свободные заряды, которые окажут влияние на результирующее электростатическое поле. Для учета этого влияния воспользуемся методом зеркальных изображений, для чего введём в расчет n фиктивных проводов, расположенных в точках зеркального изображения по отношению к заданным. Возьмём в диэлектрике произвольную точку М и определим её потенциал, используя метод наложения:  М =  М 1 ` +  М 2 +  М 3 +…+  М n , где  М 1 – составляющая потенциала, создаваемая первым проводом и его зеркальным изображением,  М 2 - составляющая, создаваемая вторым проводом и его зеркальным изображением и т.д. Будем полагать, что высоты подвеса проводов намного больше их радиусов, и тогда можно считать, что электрические и геометрические оси проводов совпадают. С учетом сказанного можно записать:

где а 1 М - расстояние от точки М до оси первого провода; b 1 M – расстояние от точки М до зеркального изображения первого провода;

и т.д. Тогда

Если точку М поместить на поверхность первого провода, то его потенциал можно определить по этой формуле, если учесть, что а 1 М =r 1 , b 1 M =2h 1 , а 2 М =а 12 – расстояние между первым и вторым проводниками, b 2 M = b 12 - расстояние от первого проводника до зеркального изображения второго и т.д., то получим

Аналогично можно определить потенциалы всех проводов ЛЭП и если это сделать, то получим первую группу формул Максвелла:

В этих уравнениях Коэффициенты  кк и  к m зависят только от геометрических размеров тел, их взаимного расположения и от свойств среды, в которой они находятся. Называются они потенциальными коэффициентами, измеряются в м/Ф и все являются положительными (под знаком логарифма стоит дробь, числитель которой всегда больше знаменателя). Им можно дать такое толкование. Пусть заряды всех проводов кроме первого равны нулю, а  1 =1. Тогда первая группа формул Максвелла принимает вид:  1 = 11 ;  2 = 21 ;  3 = 31 ; …  n = n 1 . Следовательно,  11 равен потенциалу первого провода, если на нём заряд равен 1, а остальные провода заряда не имеют,  21 равен потенциалу второго провода в указанных условиях и т.д.

Первая группа формул Максвелла определяет потенциалы проводов по их зарядам. Однако на практике часто возникает обратная задача определения зарядов проводов по их потенциалам. Это можно сделать, если первую группу формул Максвелла решить относительно зарядов, полагая потенциалы проводов и коэффициенты  известными. Тогда получим вторую группу формул Максвелла:

здесь

где  - главный определитель первой группы формул Максвелла, состоящий из потенциальных коэффициентов  , а  к m – алгебраическое дополнение, получаемое из  путём вычеркивания к -ой строки, m -го столбца и умножения оставшегося определителя на

Размерность емкостных коэффициентов обратна размерности потенциальных коэффициентов, т.е. Ф/м , поскольку  km на порядок ниже главного определителя . Ёмкостные коэффициенты имеют различные знаки, а именно  кк >0, а  к m( к  m)  1 =Е , соединив его с землёй, например, через источник постоянной ЭДС (рис.11.24). Тогда на первом проводе накопится некоторый положительный заряд  1 , а точно такой же отрицательный заряд растечется по всей земле и телам, соединенным с ней. Части отрицательного заряда попадут на второй и третий проводники. Если вторую группу формул Максвелла переписать для этого опыта, то получим:  1 =  11  1 ;  2 =  21  1 ;  3 =  3 1  1 ,

откуда имеем: Ёмкостные коэффициенты можно определять экспериментальным путём. Если после зарядки системы, включить гальванометры G 1 -G 3 (рис.11.25) и замкнуть ключ, то система разрядится и в процессе разряда гальванометры измерят заряды  1 -  3 соответственно. Тогда по последним формулам, зная  1 , можно определить  11 - 31 . Следует заметить,  к m =  mк , поскольку  к m = mк из-за симметричности  относительно главной диагонали.

Вторая группа формул Максвелла неудобна в том отношении, что в ней фигурируют потенциалы проводов, а не напряжения между ними. Поэтому часто эту систему переписывают так, чтобы в правой части фигурировали напряжения между рассматриваемым проводником и всеми остальными, в том числе и землёй.

Любая строка второй группы формул Максвелла может быть записана в компактной форме

Преобразуем выражение

где

- напряжение между к -м и m -м проводами. Тогда Обозначив

получим

Придавая индексу k значения от 1 до n , распишем систему уравнений, которая получила название третей группы формул Максвелла:

Входящие в эти уравнения коэффициенты С получили название частичных ёмкостей, причем называется собственной частичной ёмкостью k -го проводника. В указанной сумме положительным является только одно слагаемое ( kk ), тем не менее С kk всегда положительна. В этом можно убедиться, проделав следующий опыт: соединим (тоненькими проводочками) все провода ЛЭП с первым и произведём зарядку этой системы, соединив её с землёй через источник постоянной ЭДС (рис.11.26). Тогда на первом проводе накопится некоторый положительный заряд  1 , а его потенциал  1 =Е >0. Первое уравнение третей группы формул Максвелла для этого опыта имеет вид (U 12 =0, U 13 =0)  1 =C 11  1 , откуда имеем

.

Собственные частичные ёмкости можно определять экспериментальным путём. Для этого достаточно после зарядки системы измерить  1 и по последней формуле вычислить С 11 . C km =-  km называется взаимной частичной ёмкостью k -го и m -го проводников, она также является положительной, поскольку  km C km определяется также как  km .

Д

ля наглядной иллюстрации частичных ёмкостей приведем два примера. Это будут совокупности частичных ёмкостей двухпроводной линии и трёхпроводной ЛЭП (рис.11.27). Исходя из этих совокупностей могут быть определены рабочие ёмкости линий. Так для двухпроводной ЛЭП

Частичные ёмкости рассчитываются не только для электростатических полей, но используются и при расчете быстропротекающих процессов (например, в электронных лампах и транзисторах – это ёмкости между их электродами), а также при расчете устройств, в основу работы которых положено использование частичных ёмкостей (например, при ёмкостном отборе мощности от высоковольтной ЛЭП).

Третья группа формул Максвелла для системы заряженных тел любой формы. Однако приведенные выше формулы определения потенциальных коэффициентов справедливы только для ЛЭП. Если тела имеют другую форму, то и формулы будут иными. В случае, когда тела имеют сложную форму не удается вывести формулы для коэффициентов  и тогда ёмкостные коэффициенты определяют опытным путём.

Электрическое поле постоянного тока в проводящей среде

Проводящей называется среда, содержащая свободные заряды. Если в такой среде создать электрическое поле с напряженностью Е , то на каждый из свободных зарядов q будет действовать сила

Под действием этой силы свободные заряды начнут двигаться, причем упорядоченно. Упорядоченное же движение частиц, несущих на себе заряды, есть ток. Таким образом, в проводящей среде возникает ток, если в ней создано электрическое поле. Существует правда несколько видов тока и ток, протекающий по проводящей среде принято называть током проводимости. Следует упомянуть, что свободными зарядами являются электроны в металлах и ионы в жидкостях и газах. В процессе перемещения свободные заряды испытывают многочисленные столкновения с другими частицами тела, находящимися в тепловом движении. Эти столкновения затрудняют упорядоченное движение носителей зарядов и являются причиной сопротивления, оказываемого средой протеканию тока. Если бы этих столкновений не было, то не было бы и сопротивления, что имеет место в сверхпроводниках. Свойство среды, определяющее её способность проводить электрический ток характеризуется удельной проводимостью  . Она зависит от физических свойств проводящего материала и от температуры, а измеряется в См/м =1/Ом * м .

Основной величиной, характеризующей электрическое поле в проводящей среде (далее -поле в проводящей среде), является вектор плотности тока Его направление такое же как и вектора Е (понятно из физики явлений), величина определяется как

в предположении, что элементарный ток i перпендикулярен элементарной площадке s . Измеряется  в А/м 2 .

В теории поля в проводящей среде широко используется понятие тока I , представляющего собой поток вектора  :

, где S - поверхность, через которую определяется ток. В случае, когда  =const и векторы  и ds совпадают по направлению, I = S .

Законы Ома, Кирхгофа и Джоуля-Ленца в дифференциальной форме

Выделим мысленно из проводящей среды объём V в виде цилиндра очень малых размеров (рис.11.28). Пусть его длина l , поперечное сечение s .

Расположим этот цилиндр так, чтобы его образующая совпадала с направлением векторов Е и  . В силу малости объёма V можно считать, что векторы Е и  неизменны во всех его точках. Тогда ток, протекающий по телу цилиндра:

где - единичный вектор, имеющий такое же направление как и векторы Е ,  и s . Напряжение между основаниями цилиндра:

Сопротивление цилиндрического объёма

В соответствии с законом Ома в интегральной форме

или

или

Это и есть закон Ома в дифференциальной форме. Это выражение называется дифференциальной формой закона полного тока по той причине, что даёт точечную характеристику поля: в конкретной точке связывает плотность тока и напряжённость поля. Это выражение справедливо для областей поля, не занятых источниками ЭДС. А в областях, занятых источниками, кроме «кулонова» (электростатического) поля, существует ещё так называемое стороннее электрическое поле. Действительно мы знаем, если в электростатическое поле внести проводник, то в нем произойдет перемещение свободных зарядов. Причем они переместятся настолько, что создаваемое ими поле полностью скомпенсирует внешнее поле. Для того чтобы в проводнике длительно протекал ток необходимо наличие электрического поля, силы которого непрерывно перемещали бы свободные заряды. Такое поле может быть создано и поддерживаться силами неэлектрического происхождения (термоэлектрическими, химическими и т.д.), Иными словами стороннее поле всегда связано с источником энергии, который преобразует какую-либо энергию в электричество. Напряженность стороннего поля Е стор определяется как предел отношения силы, действующей на заряд, стремящийся к нулю, со стороны стороннего поля к величине этого заряда. Если в проводнике действуют одновременно и «кулоново» и стороннее поле, то напряженность результирующего поля будет

. И тогда выражение закона Ома принимает вид

Это выражение называется обобщенным законом Ома в дифференциальной форме или вторым законом Кирхгофа.

Если в проводящей среде выделить некоторый замкнутый объём, по которому протекает постоянный ток, то понятно, что ток, который войдет в объём, должен равняться току, вышедшему из него иначе в этом объёме происходило бы накопление или уменьшение электрических зарядов, что опытом не подтверждается. Иными словами сумма входящих и выходящих из объёма токов равна нулю, что математически записывается так

Это соотношение останется справедливым, если взять предел отношения потока вектора  к стремящемуся к нулю объёму, ограниченному поверхностью интегрирования

или

. Это выражение называется первым законом Кирхгофа в дифференциальной форме. Это уравнение говорит о том, что в любой точке поля в проводящей среде нет ни стока, ни истока линий вектора  , или линии вектора  являются линиями непрерывными, замкнутыми сами на себя. Поэтому данное уравнение называют ещё уравнением непрерывности линий вектора  .

Если по какому –либо проводнику с сопротивлением R протекает постоянный ток I , в нем выделяется мощность Р= I 2 R . Определим мощность, выделяющуюся в единице объёма проводящей среды

В качестве объёма V возьмем цилиндр рис.11.28. В этом цилиндре

. Его сопротивление

и объём

. Тогда

Это и есть закон Джоуля-Ленца в дифференциальной форме. Мощность тепловых потерь в объёме конечных размеров может быть определена по формуле

Граничные условия в поле в проводящей среде

Выясним какие условия выполняются при переходе тока из среды с одной удельной проводимостью в среду с другой проводимостью. На границе, разделяющей две различные проводящие среды выполняются два условия, которые сформулируем одним предложением: для всех точек, являющихся общими для этих сред равны по величине тангенциальные составляющие вектора Е и нормальные составляющие вектора  . Для доказательства первого условия окружим любую точку, находящуюся на границе между средами, бесконечно малым (длина - dl ) плоским (высота бесконечно мала по сравнению с длиной) контуром mnpq и составим выражение циркуляции вектора Е для этого контура (рис.11.29). Сторона mn находится в верхней среде и, если контур обходить по часовой стрелке, то составляющая циркуляции вдоль этой стороны .Аналогично для стороны pq , находящейся во второй среде . В последнем выражении минус стоит потому, что тангенциальная составляющая Е 2 t и вектор dl направлены в противоположные стороны. Составляющими циркуляции вектора Е вдоль сторон pm и nq можно пренебречь в силу малости этих сторон. Для потенциального поля, которым является и поле в проводящей среде,

. Тогда

или

, что и требовалось доказать.

Для доказательства второго условия возьмем произвольную точку на границе и окружим её бесконечно малым плоским объёмом в виде параллелепипеда (рис.11.30) и применим к нему принцип непрерывности линий тока в интегральной форме

. Через боковые грани потоком вектора  можно пренебречь из-за малости этих граней, а через верхнюю и нижнюю – соответственно и . Следовательно,

или

.

Определим связь между углами  1 и  2 , которые по аналогии с оптикой получили названия углов падения и преломления. Из рис.11.30 вытекает: , так как и . Если ток переходит из среды с большой проводимостью  2 (металл) в среду с малой проводимостью  1 (допустим земля), то

, т.е.

. Иными словами в среде с малой проводимостью линии тока практически перпендикулярны к границе.

Аналогия между полем в проводящей среде и электростатическим полем

По своей природе электростатическое поле и поле постоянного тока в проводящей среде совершенно различны. Электростатическое поле создается неподвижными и неизменными во времени зарядами, а поле в проводящей среде – это поле зарядов, имеющих упорядоченное движение под действием внешнего источника. Тем не менее между этими двумя полями может быть проведена формальная аналогия, которая заключается в следующем.

1.Электростатическое поле в областях, не занятых зарядом, и поле в проводящей среде в областях, свободных от источников ЭДС, описываются одним и тем же уравнением – уравнением Лапласа. Для электростатического поля мы уже показывали, что

. Покажем это для поля в проводящей среде, в котором

, а Тогда

Если среда однородна и изотропна, то  является постоянной величиной, ее можно вынести за знак дивергенции, которая и должна давать ноль, т.е.

Поскольку поле в проводящей среде является потенциальным, то

. Тогда

или Это и есть уравнение Лапласа.

2. В каждом из этих полей могут быть найдены сходные величины, основные из которых указаны в табл.

3. В этих полях выполняются одинаковые граничные условия для сходных величин: в электростатике Е 1 t =Е 2 t и D 1 n =D 2 n , в проводящей среде Е 1 t =Е 2 t и  1 n =  2 n .

Но если два поля удовлетворяют одному и тому же уравнению и в них выполняются одинаковые граничные условия для сходных величин, то поля тождественны, т.е. в них одинаковы совокупности силовых и эквипотенциальных линий при одинаковой форме граничных поверхностей. Эта формальная аналогия очень широко используется на практике. Так, если какое-либо электростатическое поле изучено, то все сведения о нем могут быть перенесены на геометрически подобное поле в проводящей среде. Справедлив, конечно, и обратный перенос. Эта аналогия лежит в основе моделирования одних полей другими (чаще всего электростатических полей – полем в проводящей среде). Указанная аналогия позволяет пользоваться формулами, полученными при расчете электростатических полей, и в случае поля в проводящей среде. В частности, формулы для проводимости между электродами, помещенными в проводящую среду, могут быть получены из формул ёмкости между такими же электродами в электростатическом поле. Покажем это. Если два электрода поместить в проводящую среду и подвести к ним питание от источника с напряжением U S . Тогда согласно теореме Гаусса в интегральной форме

А

Сравнивая выражения для G и С , видим, что они отличаются тем, что в них  и  а меняются местами. Это соотношение можно записать так

что говорит о том, что если в формуле ёмкости  а заменить на  , то получим формулу для определения G . Конечно возможен и обратный переход.

Рассмотрим конкретный пример. Изоляция коаксиального кабеля не бывает идеальной. Практически она обладает некоторой хотя и очень малой удельной проводимостью  . В связи с этим, если к кабелю подвести напряжение U , то по изоляции начнет замыкаться ток, получивший название тока утечки (рис.11.33). Этот ток можно определить по формуле I=UG , где G - проводимость изоляции между жилой и оболочкой кабеля. Ранее была выведена формула ёмкости коаксиального кабеля

Тогда на основании аналогии

Расчет заземлителей

Для осуществления соединения каких-либо точек цепи с землей в неё зарывают металлические проводники, к которым и присоединяют соответствующие точки цепи. Система таких зарытых в землю проводников и называется заземлителем. Назначение заземлителей многообразное. Бывают рабочие заземления (трамвай), бывают защитные заземления и т. д. При коротких замыканиях (КЗ) и других авариях, а иногда и в нормальном режиме (трамвай) через заземлитель протекает ток, который растекается по земле и при этом встречает некоторое сопротивление, которое и называется сопротивлением заземлителя. Сопротивление заземлителя R з (сопротивление всей земли растеканию тока) является его первой важной характеристикой. Второй важной характеристикой является шаговое напряжение U ш – разность потенциалов между двумя точками, расположенными на поверхности земли и отстоящими друг от друга на расстоянии шага человека. Поскольку при КЗ ток, протекающий по заземлителю может иметь большие значения, то он вдоль поверхности земли может создавать вблизи от места заземления шаговое напряжение, опасное для жизни человека. Известно много случаев гибели людей от шагового напряжения. Отсюда понятна важность умения его рассчитывать. При расчете заземлителей (R з и U ш ) принимаются некоторые допущения, главными из которых являются

Не учитывается сопротивление электродов, зарытых в землю.

В земле линии тока не уходят в бесконечность, а собираются у другого электрода. Это не учитывается поскольку мало сказывается на распределении тока вблизи рассматриваемого электрода, где плотность тока имеет наибольшее значение, и на величине соответствующего ему сопротивления заземлителя.

Шаговое напряжение у такого заземлителя отсутствует из-за далёкого расположения поверхности земли.

Шаговое напряжение где l ш - длина шага человека, которая в соответствии с Правилами Безопасности должна приниматься равной 0,8 м .

Заземлитель в виде шара, неглубоко зарытого в землю

Если заземлитель в виде шара расположен близко от поверхности земли (рис.11.36), то линии тока искажаются. Для учета этого искажающего влияния поверхности земли можно применить метод зеркальных изображений. Линии тока у поверхности земли должны быть к ней касательны (не содержать нормальных составляющих). Это условие будет выполнено, если верхнее полупространство мысленно заполнить проводящей средой с такой же как у земли удельной проводимостью и поместить в эту среду электрод, являющийся зеркальным изображением относительно поверхности земли действительного электрода. Ток, подходящий к мнимому электроду должен быть таким же по величине и знаку как и ток действительного электрода. Поле такого заземлителя можно определить методом наложения от действия фактического заземлителя и его зеркального изображения. Потенциал любой точки поля будет

где поле . Поле Электростатическое поле создано... 13 Тема: Электростатическое поле . Поле точечного заряда. Принцип суперпозиции Электростатическое поле создано точечным положительным...

1. Перечень тестовых заданий и задач, рекомендуемых студентам для подготовки к экзаменам по разделу дисциплины Физика «Электричество и магнетизм» Тестовые задания Электростатическое поле в вакууме

   Документ

   Шарика, если в однородном электростатическом поле шарик оказался взвешенным в глицерине. Электростатическом поле направлено вертикально вверх...

2. Диэлектрики в электростатическом поле. Вектор поляризации. Электрическое смещение. Теорема Гаусса для электрического смещения. 5

   Документ

   Диполь в однородном и неоднородном электрическом поле . 3. Диэлектрики в электростатическом поле . Вектор поляризации. 4. Электрическое... 6. Электрическая ёмкость. Конденсаторы. Энергия электростатического поля Проводники и диэлектрики. Свободные и...

3. Отчет по лабораторной работе №1 «исследование электростатического поля методом моделирования в проводящей среде»

   Отчет

   Связь, выражающаяся соотношением: (1.1) В диэлектриках электростатическое поле характеризуется векто­ром электрического смещения... ­лать вывод о возможности моделирования электростатического поля электрическим полем в проводящей среде, если соблюдается...

4. На каком рисунке правильно изображена картина линий электростатического поля точечного положительного заряда?

   Документ

   Напряжённости электростатического поля заряда Q в точке C равен EC. Чему равен модуль напряжённости электростатического поля ... напряжённости электростатического поля заряда Q в точке С равен EС. Чему равен модуль напряжённости электростатического поля ...

Заряженной осью называется очень тонкий, теоретически бесконечно длинный проводник, несущий на себе заряд. Весь заряд оси указать невозможно (он равен бесконечности), поэтому указывается линейный заряд

, т.е. заряд, приходящийся на единицу длины оси. Пусть ось с положительным зарядомτ находится в среде с проницаемостью ε а (рис.11.15). Используя интегральную форму теоремы Гаусса, произведем расчет напряженности поля в произвольной точке, удаленной на расстояние r от оси. С этой целью проведем через данную точку замкнутую поверхность в виде цилиндра длиной l . Поток вектора Е имеет место только через боковую поверхность этого цилиндра, поскольку в точках, расположенных на его донышках векторы Е и ds перпендикулярны и их произведение равно нулю. В точках же боковой поверхности векторы Е и ds совпадают по направлению и их произведение равно произведению модулей, а модуль Е одинаков во всех этих точках в силу симметрии. С учетом сказанного имеем Внутри поверхности интегрирования заряд

. Поэтому

или

т.е. напряженность в данном поле изменяется обратно пропорционально расстоянию от оси.

Потенциал Постоянная интегрированияА зависит от того, где расположить точку с нулевым потенциалом. Следовательно, в данном поле потенциал изменяется по логарифмическому закону.

Электростатическое поле двух заряженных осей

На практике чаще всего две заряженные оси несут на себе равные по величине и противоположные по знаку заряды +E ds l r τ и -τ . Именно такой случай и рассмотрим (рис.11.16). Возьмем в поле произвольную точкуМ , положение которой будем характеризовать расстояниема до положительной оси и расстояниемb до отрицательной оси и в первую очередь рассчитаем в ней напряженность поля, используя метод наложения:

где

- составляющие, создаваемые положительно и отрицательно заряженной осью соответственно. Величины этих составляющих могут быть определены по формулам, взятым из предыдущей темы, а именно:

Аналогично для потенциала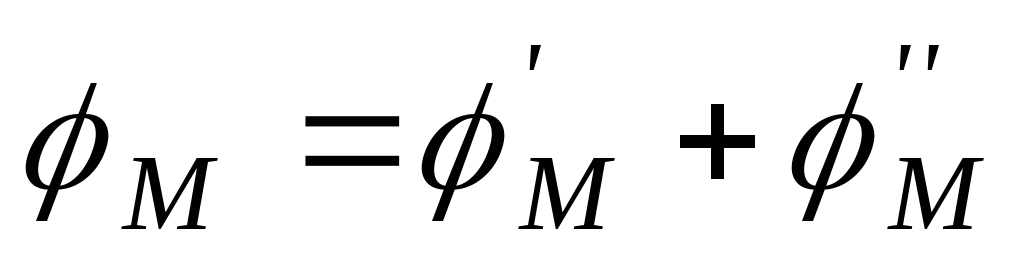

, где. ТогдаИз последнего выражения следует, что совокупность точек, для которых

, представляет собой эквипотенциаль. Из геометрии известно, что геометрическим местом точек, отношение расстояний от которых до двух заданных точек является величиной постоянной, есть окружность (теорема Аполлония). Поэтому эквипотенциали в поле двух заряженных осей являются окружностями. Для построения эквипотенциальной линии, проходящей через точкуМ , проводим биссектрисы внутреннегоаМ b н внешнегорМа углов. Точки пересечения этих биссектрис с линией, проведенной через оси, (т.1 и т.2), а также т.М являются тремя точками этой эквипотенциали. Центр этой окружности находится в точке, расположенной посредине между т.1 и т.2.

Электростатическое поле и ёмкость двухпроводной линии электропередачи (ЛЭП)

Пусть провода ЛЭП имеют одинаковый радиусr о , расположены на расстоянииd друг от друга и находятся в среде с проницаемостью ε а (рис.11.17). Если левому проводу сообщен зарядτ на единицу длины, правому -τ , то в пространстве между проводами возникнет электростатическое поле, которое можно представить в виде части поля двух заряденных осей. Действительно, поскольку провода металлические, то внутри них поля нет (Е =0), а потенциал всех точек каждого провода одинаков, т.е. поверхность каждого провода является эквипотенциальной. Поэтому две заряженные оси, расположенные в т.m иn , создадут такую же картину поля как и двухпроводная ЛЭП, если т.m иn расположить так, чтобы поверхности проводов были для них эквипотенциалями. Точкиm иn принято называть электрическими осями в отличие от геометрических осей (точки О и О 1). Смещение электрических и геометрических осей (x ) в силу симметрии одинаково в левом и правом проводе. Для определения величиныx возьмём точки 1 и 2 и запишем выражения потенциалов этих точек в поле двух заряженных осей, расположенных в т.m иn .

Так как т. 1 и 2 расположены на поверхности одного и того же провода, то φ 1 =φ 2 , следовательно,

Решая это равенство относительноx , получим

В этом выражении при отсчетеx от т.О плюс определяет положение т.n , а минус – положение т.m . Еслиd >> r o , тоx 1 =0,x 2 =d , т.е. электрические и геометрические оси совпадают (нет смещения осей). Частоx не вычисляют по полученной выше формуле, а получают графическим путем. Для этого проводят общую касательную к поверхности проводников, делят расстояние между точками касания (PиQ) пополам (т. С) и проводят дугу окружности, проходящей через т. Р иQи имеющей центр в т. С. Точки пересечения этой окружности с линией О 1 О дают положение электрических осей. Из геометрического определения положения электрических осей так же видно, что приd >> r o т. m иn сольются с т.О и О 1 .

После того, как определено смещение осей, задача сведена к предыдущей.

Перейдем к вопросу о ёмкости двухпроводной линии. Если два проводника разделены диэлектриком и несут на себе равные по величине и противоположные по знаку заряды, то в пространстве между ними создается электростатическое поле. Пусть напряжение между проводниками равно U . Тогда ёмкостью между проводниками называется отношение абсолютной величины заряда на одном из тел к напряжению между ними:

. Единица измерения ёмкости – Фарада (

). Так как напряжение между телами пропорционально заряду на них, то ёмкость ни от заряда, ни от напряжения не зависит, а зависит она от конфигурации и геометрических размеров тел, их взаимного расположения и от свойств диэлектрика, в котором они находятся. Существуют устройства, предназначенные для получения определенной величины ёмкости – это конденсаторы, однако ёмкостью обладают не только конденсаторы, а всякие два тела, способные нести на себе равные по величине и противоположные по знаку заряды.

Определим ёмкость двухпроводной линии. Напряжение между проводами Заряд одного из проводовq = τl . Тогда

Часто определяют ёмкость единицы длины линии

А еслиd >> r o , тоx =0 и

Из полученных формул видно, что ёмкость действительно зависит от размеров линии и свойств среды, в которой находятся провода, в частности, если увеличивать расстояниеd между проводами, то ёмкость будет уменьшаться.

Электростатическое поле и ёмкость коаксиального кабеля

Коаксиальный кабель представляет собой два металлических соосных цилиндра, расположенных один внутри другого и изолированных друг от друга диэлектриком с проницаемостьюε а (рис.11.18). Такой кабель широко применяется на высоких частотах. Пусть внутренний цилиндр, который называется жилой, несёт на себе заряд +τ , а наружный цилиндр (оболочка) – заряд –τ . Тогда возникнет электростатическое поле, расчёт которого произведём для отдельных областей кабеля. Внутри жилы (0>r > r 1) поля нет, так как жила проводящая, т.е.E =0,φ =const. Для определения напряжённости поля в пространстве между жилой и оболочкой воспользуемся теоремой Гаусса:

В качестве поверхности интегрирования возьмём цилиндр радиусаr и длинойl . Поток вектораЕ через донышки этого цилиндра равен нулю (векторыЕ иds перпендикулярны), а через его боковую поверхность



Тогда

Так какЕ имеет только радиальную составляющую, то

Для всех точек оболочки кабеля (r 2 < r < r 3)E =0,φ =const, так как она проводящая.За пределами кабеля (r 3 <∞)

поэтомуE =0, φ =const. Таким образом в данном устройстве поле имеется только в пространстве между жилой и оболочкой.

Ёмкость коаксиального кабеля С =гдеq = τl ,a

Тогда

, а

Электростатическое поле и ёмкость однослойного и двухслойного плоских конденсаторов

Однослойный плоский конденсатор состоит из двух металлических пластин сечением S , расположенных на расстоянииd друг от друга (рис.11.19). Определим закон измененияЕ ,D иφ , если к нему подведено напряжениеU . Если размеры пластин (длина, высота) намного большеd , то можно пренебречь краевым эффектом (искажением поля на краях пластин) и считать его электростатическое поле равномерным, т.е. при всех значенияхх напряженность поля одна и та же. Тогда

откуда

а D =ε a E =

Так как

аφ зависит только отх (плоскостьyoz- эквипотенциаль), то

или

Для определения постоянной интегрированияА примем, что потенциал правой пластины равен нулю, а левой равенU , т.е. прих =0φ= U . ТогдаА= U и

т.е.φ изменяется по линейному закону в зависимости отх .

Определим ёмкость плоского конденсатора С =гдеU = Ed . Для определения заряда, например, левой пластины воспользуемся теоремой Гаусса:

причем

Определим поток вектораD через замкнутую поверхность, охватывающую эту пластину (рис.11.19)

так как векторыD и ds совпадают по направлению и D имеет одно и тоже значение во всех точках, находящихся внутри конденсатора. Следовательно, q = DS = ε a ES и

Двухслойный конденсатор (рис.11.20) отличается от предыдущего тем, что изоляция между пластинами состоит из двух слоёв с проницаемостями ε 1а и ε 2а. Если по-прежнему пренебречь краевым эффектом, то поле такого конденсатора характерно тем, что в каждом слое оно является однородным с напряженностями Е 1 и Е 2 соответственно. Тогда

Однако этого уравнения недостаточно для определенияЕ 1 и Е 2 . Для составления второго уравнения используем граничные условия. Известно, что на границе раздела двух разных диэлектриков равны нормальные составляющие вектора электростатической индукции (D 1 n = D 2 n ). Если учесть, что в нашем случае эти векторы перпендикулярны к границе, то это равенство примет вид D 1 =D 2 или ε 1 а Е 1 = ε 2 а Е 2 . Это и будет второе уравнение. Решая совместно эти уравнения, получим

Определим закон изменения потенциала:

Постоянную интегрирования А 1 определим из условия, что при х =0 φ 1 = U (А 1 =U ), а А 2 – из условия, что при х =d 1 φ 1 =φ 2 (или φ 2 =0 при х =d 1 +d 2). Из полученных формул видно, что потенциал изменяется по линейному закону. На рис.11.21 показаны графики зависимости от х индукций, напряженностей и потенциалов.

Ёмкость такого конденсатора определяется как эквивалентная двух последовательно соединенных ёмкостей:

где

ёмкость первого слоя, а

ёмкость второго слоя изоляции конденсатора.

Метод зеркальных изображений

Данный метод применяется для расчета полей, в которых имеется геометрически правильной формы граница раздела различных сред. Это искусственный расчетный метод, сущность которого заключается в том, что в расчет кроме заданных зарядов вводятся еще дополнительные или фиктивные заряды, величина и место расположения которых выбираются такими, чтобы выполнялись граничные условия. Чаще всего фиктивные заряды располагаются в точках зеркального изображения по отношению к заданным, отсюда и название метода. Дополнительные или фиктивные заряды в расчет вводятся для того, чтобы учесть влияние появляющихся в результате электростатической индукции свободные или связанные заряды.

Факт взаимодействия электрических зарядов на расстоянии можно объяснить наличием вокруг них электрического поля - материального объекта, непрерывного в пространстве и способного действовать на другие заряды.

Поле неподвижных электрических зарядов называют электростатическим.

Характеристикой поля является его напряженность.

Напряженность электрического поля в данной точке - это вектор, модуль которого равен отношению силы, действующей на точечный положительный заряд, к величине этого заряда, а направление совпадает с направлением силы.

Напряженность поля точечного заряда Q на расстоянии r от него равна

2.Передача электромагнитной энергии вдоль проводов линии.

Билет 20

1. Поле заряженной оси и цилиндра.

Под заряженной осью понимают тонкий, теоретически бесконечно длинный металлический проводник.

Под линейной плотностью заряда t понимают заряд, приходящийся на единицу длины оси.

Пусть диэлектрическая проницаемость окружающей среды равна e a .

Для нахождения напряженности поля в некоторой точке, удаленной на расстояние r от оси, проведем через точку цилиндрическую поверхность так, чтобы ее ось совпала с заряженной осью (рис. 15.6).

Рис. 15.6. К определению поля заряженной оси

Используем теорему Гаусса, которая применима к замкнутой поверхности (боковая поверхность цилиндра и два его основания). Поток вектора имеется только через боковую поверхность. Направление и на боковой поверхности в каждой точке совпадают, поэтому

Напряженность в поле заряженной оси изменяется обратно пропорционально расстоянию r точки от оси.

Потенциал изменяется по экспоненциальному закону.

Электрическая емкость определяется как отношение заряда к разности потенциалов между телами. Рассчитаем емкость двух соосных цилиндров (рис. 15.7).

Рис. 15.7. Разрез двух соосных цилиндров

Напряжение между поверхностями цилиндров

Емкость цилиндрического конденсатора будет равна

(15.27)

2. Излучение электромагнитной волны. Уравнение Даламбера.

3. Будем исходить из уравнения Максвелла . Домножим обе части на и учтем, что и . получим:

4. .

5. Учтем, что и . Тогда получим

6.

7.

9. Пользуясь неоднозначностью потенциалов, определяемых с точностью до калибровочного преобразования, для максимального упрощения наложим на них условие:

10. (28.2)

11. И тогда из (28.1) получим уравнение Даламбера:

12. (28.3)

13. Условие (28.1) называется условием калибровки Лоренца. Получим теперь уравнение для скалярного потенциала следующим образом:

14. и учтем, что . Тогда

15. .

16. Из (28.2): . Тогда получим

17. (28.4)

18. Уравнение (28.4) тоже уравнения Даламбера. Следовательно, для скалярного и векторного потенциалов получили одно и тоже уравнение.

19. (28.5)

20. Где - скорость электромагнитных волн в среде. Уравнение (28.5) – уравнение гиперболического типа и описывает волновой процесс, т. е. волны, распространяющиеся в пространстве со скоростью . В одномерном случае при решение (28.5) можно представить в виде суммы двух функций:

21. . (28.6)

22. Которое описывает волны, распространяющиеся в двух противоположных направлениях. Функция представляет собой волну, движущуюся в направлении положительных значений оси Ох со скоростью , а - в противоположном направлении.

23. Рассмотрим решение волнового уравнения в сферически симметричном случае, т. е. считая, что в (28.5) F=0 , а Ф=Ф(R ), где R – расстояние от начала координат до рассматриваемой точки. В этом случае Ф от углов не зависит и оператор Лапласа имеет вид

25. Поэтому волновое уравнение для Ф записывается в виде

26. . (28.8)

27. Решением этого уравнения для , как и в предыдущем случае, являются произвольные функции от аргумента и , т. е. общее выражение для Ф таково:

28. . (28.9)

29. Функция Представляет волну, движущуюся в радиальном направлении от начала координат со скоростью . Форма волны при этом не изменяется, а амплитуда уменьшается как 1/R . Эта волна называется расходящейся. Функция представляет сходящуюся к началу координат волну.

30. Потенциалы поля, а следовательно, и сами поля распространяются в свободном пространстве со скоростью . В вакууме , , поэтому скорость распространения полей равна скорости света . Таким образом Электромагнитные волны и всякие изменения электрического и магнитного поля распространяются в вакууме со скоростью света . А это означает, что электромагнитные взаимодействия распространяются со скоростью света. Например, если два точечных заряда покоятся на расстоянии R друг от друга и один из зарядов в некоторый момент сдвинут со своего места, то другой заряд «почувствует» этот сдвиг лишь спустя время .

Билет 21

1. Электростатическое поле и ёмкость коаксиального кабеля

К оаксиальный кабель представляет собой два металлических соосных цилиндра, расположенных один внутри другого и изолированных друг от друга диэлектриком с проницаемостью ε а (рис.11.18). Такой кабель широко применяется на высоких частотах. Пусть внутренний цилиндр, который называется жилой, несёт на себе заряд +τ , а наружный цилиндр (оболочка) – заряд –τ . Тогда возникнет электростатическое поле, расчёт которого произведём для отдельных областей кабеля. Внутри жилы (0>r>r 1) поля нет, так как жила проводящая, т.е.E =0, φ =const. Для определения напряжённости поля в пространстве между жилой и оболочкой воспользуемся теоремой Гаусса: В качестве поверхности интегрирования возьмём цилиндр радиуса r и длиной l . Поток вектора Е через донышки этого цилиндра равен нулю (векторы Е и ds перпендикулярны), а через его боковую поверхность Тогда Так как Е имеет только радиальную составляющую, то

Для всех точек оболочки кабеля (r 2 3) E=0, φ=const, так как она проводящая. За пределами кабеля (r 3 <∞) поэтому E=0, φ=const. Таким образом в данном устройстве поле имеется только в пространстве между жилой и оболочкой.

Ёмкость коаксиального кабеля С= где q=τl, a

Тогда , а

2. Переменное электромагнитное поле в проводящей среде.

Проводящая среда предполагается однородной и изотропной. Уравнения Максвелла для проводящей среды в комплексной форме записи.

	(4.14)
(4.15)

Уравнения записаны для мгновенных значении. Если и во времени изменяются по синусоидальному закону, то можно воспользоваться символическим методом для их записи. И будем обозначать:

Комплекс действующего значения синусоидального изменяющегося вектора напряженности (проекция вектора на любую ось изменяется по синусоидальному закону).

Очевидно, что однократное дифференцирование вектора по времени приводит к умножению его комплексной амплитуды или комплекса действующего значения на , а двукратное умножение на .

Итак, уравнения Максвелла в комплексной форме с учетом :

(4.14):		(4.16)
(4.15):	(4.17)

Рассмотрим особенности распространения электромагнитной волны в проводящей среде с проводимостью и магнитной проницаемостью .

В проводящей среде даже при весьма высоких частотах . В настоящее время наука не располагает точными данными о числовом значении относительной магнитной проницаемости для металлов. Имеются лишь сведения, что порядок для металлов такой же, как и для большинства диэлектриков, то есть от нескольких единиц до нескольких десятков.

Например, для меди . Найдем, во сколько раз ток проводимости будет больше тока смешения при :

то есть даже на очень высоких частотах ток проводимости гораздо больше тока смещения.

(4.16):

(4.18)

Уравнения (4.17) и (4.18) представляют собой уравнения с 2-мя неизвестными: и . Проведем их совместное решение. С этой целью возьмем ротор от уравнения (4.18):

Учтем, что , поэтому .

С учетом (4.17): ,

(4.19)

уравнение (4.19) является дифференциальным относительно . В самом общем случае, когда зависит от 3х или даже от 2х координат, решение (4.19) – сложно. Поэтому ограничимся рассмотрением решения (4.19) для частного случая - для плоской и для цилиндрической электромагнитной волны

Билет

(1)Поле и емкость плоского конденсатора.

Конденсаторы состоят из двух или более близко расположенных друг к другу проводников (обкладок), разделенных слоем диэлектрика (рис. 1), причем толщина слоя диэлектрика между проводниками значительно меньше размеров самих проводников.

При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников.

Обкладкам конденсатора сообщают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов, так как разноименные заряды притягиваются и поэтому располагаются на внутренних поверхностях пластин.

Под зарядом конденсатора понимают заряд одной пластины.

Электроемкостью конденсатора называют физическую величину, численно равную отношению заряда конденсатора к разности потенциалов между его обкладками:

Обозначим площадь одной обкладки S, расстояние между ними d.

Следовательно, емкость плоского конденсатора

Поле плоского конденсатора можно рассматривать как совокупность полей двух бесконечных разноименно заряженных плоскостей (рис. 2, а и б). Напряженность поля (рис. 2, в) можно найти по принципу суперпозиции

- напряженность поля конденсатора, где - поверхностная плотность заряда на обкладках конденсатора.

2. Плоская волна в проводящей среде. Преломление и отражение плоской волны.

Плоская волна в проводящей среде

Рассмотрим распространение плоской электромагнитной волны в проводящей среде, которая простирается теоретически в бесконечность.

Электромагнитная волна проникает из диэлектрика в проводящую среду и распространяется в ней. Так как среда теоретически бесконечна и падающая волна не встречает границы, которая изменила бы ее распространение, то отраженной волны в данном случае не возникает.

Так как и : ,

Постоянную интегрирования найдем из пограничных условий. Если обозначить напряженность магнитного поля на поверхности проводящей среды через , то при и :

,

Чтобы записать выражения для линейных значений и необходимо правые части и умножить на и взять мнимые части от полученных произведений. Получим:

	(4.24)
	(4.25)

Проанализируем выражения (4.24) и (4.25)

амплитуда

амплитуда .

По мере увеличения я множитель уменьшается по показательному закону, следовательно, по мере проникновения электромагнитной волны в проводящую среду, амплитуды и уменьшаются по показательному закону.

Основной задачей электростатики является определение величины и направ­ле­ния вектора напряженности в каждой точке поля, создаваемого либо системой неподвижных точечных зарядов, либо заряженными поверхностями произвольной формы. Рассмотрим первый случай, когда поле создано системой зарядов q 1 , q 2 ,..., q n . Если в какую-либо точку этого поля поместить пробный заряд q 0 , то на него со стороны зарядов q 1 , q 2 ,..., q n будут действовать кулоновские силы . Со­гласно принципу независимости действия сил, рассмотренного в механике, равно­дей­ствующая сила равна их векторной сумме

.

Используя формулу напряженности электростатического поля, левую часть ра­венства можно записать: , где - напряженность результирующего поля, создаваемого всей системой зарядов в точке, где расположен пробный заряд q 0 . Пра­вую часть равенства соответственно можно записать. Полученная формула применима и для расчета электростатических полей за­ря­женных тел произвольной формы так как любое тело можно разделить на очень малые части, каж­дую из которых можно считать точечным зарядом q i . Тогда расчет в любой точке пространства будет аналогичен выше приведенному.

(2)………………………………………..

Длина волны λ - это расстояние между двумя ближайшими точками оси X, в которых колебания значений поля происходят в одинаковой фазе

(в частности - между двумя ближайшими максимумами поля, как на рис. 5).

Частота, с которой меняются значения E и B в данной точке пространства, называется частотой электромагнитной волны; она совпадает с частотой ν колебаний излучающего заряда. Длина электромагнитной волны λ, её частота ν и скорость распространения c связаны стандартным для всех волн соотношением: c = λν.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 25

1. Расчет электрической емкости.

2. Эффект близости. Поверхностная закалка индукционным методом.

Билет №26

1. Поле точечного заряда в однородной среде.

Электрическое поле создается как неподвижными, так и движущимися зарядами. О наличии электрического поля можно судить, прежде всего, по его способности оказывать силовое действие на электрические заряды, движущиеся и неподвижные, а также по способности индуцировать электрические заряды на поверхности проводящих нейтральных тел.

Поле, создаваемое неподвижными электрическими зарядами, называют стационарным электрическим, или электростатическим полем . Оно представляет собой частный случай электромагнитного поля, посредством которого осуществляются силовые взаимодействия между электрически заряженными телами, движущимся в общем случае произвольным образом относительно системы отсчета.